► By a sequence, we mean an arrangement of number in definite order according to some mile. Also, we define a sequence as a function whose domain is the set of natural numbers or some subsets of the type {1, 2, 3, …, k}. A sequence containing a finite number of terms is called a finite sequence. A sequence is called infinite if it is not a finite sequence.
► Let a1, a2, a3, … be the sequence, then the sum expressed as a1+a2+a3+⋯ is called series. A series is called finite series if it has got finite number of terms.
► An arithmetic progression (A.P.) is a sequence in which terms increase or decrease regularly by the same constant. This constant is called common difference of the A.P. Usually, we denote the first term of A.P. by a, the common difference by d and the last term by ℓ. The general term or the nth term of the A.P. is given by an=a+(n-1)d.
The sum Sn of the first n terms of an A.P. is given by
► The arithmetic mean A of any two numbers a and b is given by ½n(a+b). Thus, the sequence a, A, b is an arithmetic sequence.
► A sequence is said to be a geometric progression or GP., if the ratio of any term to its preceding term is same throughout. This constant factor is called the common ratio. Usually, we denote the first term of a GP. by a and its common ratio by r. The general or the nth term of G.P. is given by an=a⋅rn-1.
The sum Sn of the first n terms of GP. is given by

► The geometric mean (G.M.) of any two positive numbers a and b is given by √a⋅b. Thus, the sequence a, G, b is a G.P.
In this chapter, you have studied the following points:
1. An arithmetic progression (AP) is a list of numbers in which each term is obtained by adding a fixed number d to the preceding term, except the first term. The fixed number d is called the common difference.
The general form of an AP is a, a+d, a+2d, a+3d, …
2. A given list of numbers a1, a2, a3, … is an AP, if the differences a2–a1, a3–a2, a4–a3, …, give the same value, i.e., if ak+1–ak is the same for different values of k.
3. In an AP with first term a and common difference d, the nth term (or the general term) is given by an=a+(n-1)d.
4. The sum of the first n terms of an AP is given by:
5. If ℓ is the last term of the finite AP, say the nth term, then the sum of all terms of the AP is given by:
A Note To The Reader
If a, b, c are in AP, then b=½(a+c) and b is called the arithmetic mean of a and c.
1. nth term of General Term of an Arithmetic progression.
2. Arithmetic means between a and b
3. Sum of the First n terms of an arithmetic series.
(i) Sn=½n[2a+(n-1)d]
(ii) Sn=½n(a+ℓ) when last term ‘ℓ’ is known.
4. General or nth term of a G.P
5. Geometric means between a and b
6. Sum of n terms of a Geometric Series
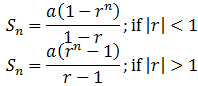
7. Sum of an infinite Geometric Series
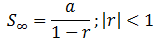
| Big Ideas | Applying the Big Ideas |
|---|---|
| ▪ An arithmetic sequence is related to a linear function and is created by repeatedly adding a constant to an initial number. An arithmetic series is the sum of the terms of an arithmetic sequence. | This means that: ▪ The common difference of an arithmetic sequence is equal to the slope of the line through the points of its related linear function. ▪ Rules can be derived to determine the nth term of an arithmetic sequence and the sum of the first n terms of an arithmetic series. |
| ▪ A geometric sequence is created by repeatedly multiplying an initial number by a constant. A geometric series is the sum of the terms of a geometric sequence. | ▪ The common ratio of a geometric sequence can be determined by dividing any term after the first term by the preceding term. ▪ Rules can be derived to determine the nth term of a geometric sequence and the sum of the first n terms of a geometric series. |
| ▪ Any finite series has a sum, but an infinite geometric series may or may not have a sum. | ▪ The common ratio determines whether an infinite series has a finite sum. |
| Skill | Description | Example |
|---|---|---|
| Determine the general term, tn, for an arithmetic sequence. (1.1, 1.2) |
A rule is: where t1 is the first term, d is the common difference, and n is the number of terms. |
For this arithmetic sequence: -9, -3, 3, 9, … the 20th term is: t20=-9+6⋅(19) t20=105 |
| Determine the sum of n terms, Sn, for an arithmetic series. (1.2) | When n is the number of terms, t1 is the first term, tn is the nth term, and d is the common difference One rule is: Sn=½n(t1+tn) Another rule is: |
For this arithmetic series: 5+7+9+11+13+15+17; the sum of the first 7 terms is: S7=½⋅7⋅(22) S7=77 |
| Determine the general term, tn, for a geometric sequence. (1.3, 1.4) | A rule is: where t1 is the first term, r is the common ratio, and n is the number of terms. |
For this geometric sequence: 1, -0.25, 0.0625, … the 6th term is: t6=(-1)5⋅(0.25)5 t6=-0.000 976 5… |
| Determine the sum of n terms, Sn, of a geometric series. (1.4) | A rule is: where t1 is the first term, r is the common ratio, and n is the number of terms. |
For this geometric series: 4, 2, 1, … the sum of the first 10 terms is: or approximately 8 |
| Determine the sum, S∞, of a convergent infinite geometric series. (1.6) |
When r is between-1 and 1, use this rule: where t1 is the first term and r is the common ratio. |
For this geometric series: the sum is:  |





