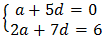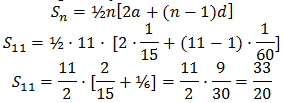Problem 1. Find the sum of first 51 terms of an arithmetic sequence whose second and third terms are 14 and 18 respectively.
Solution:
Let a be the first term and d be the common difference of the arithmetic sequence. Then,

d=a₃–a₂=18-14=4
Given a₂=14.
[a_n=a+(n-1)d]
a+d=14
a+4=14
a=14-4=10
Using the formula, S_n=½n[2a+(n-1)d], we get
S₅₁=½⋅51⋅[2⋅10+(51-1)⋅4]
=½⋅51⋅(20+200)
=½⋅51⋅220
=5610.
Hence, the required sum is 5610.

P2. The 13th terms of an arithmetic sequence is 4 times its 3rd term. If its 5th term is 16, Find the sum of its first 10 terms.
Solution:
Let a be the first term and d be the common difference of the arithmetic sequence. Then, a₁₃=4⋅a₃ (Given).

[a_n=a+(n-1)d]a+12d=4(a+2d)
a+12d=4a+8d
3a=4d … (1)
Also, a₅=16 (Given)
a+4d=16 … (2)
Solving (1) and (2), we get
a+3a=16
4a=16
a=4
Putting a=4 in (1), we get
4d=3⋅4=12
d=3Using the formula, S_n=½n[2a+(n-1)d], we get
S₁₀=½⋅10⋅[2⋅4+(10-1)⋅3]
=5⋅(8+27)
=5⋅35
=175.
Hence, the required sum is 175.

P3. The 16th term of an arithmetic sequence is 5 times its 3rd term. If its 10th term is 41, find the sum of its first 15 terms.
Solution:
Let a be the first term and d be the common difference of the arithmetic sequence. Then,

a₆=5⋅a₃ (Given)
[a_n=a+(n-1)d]
a+15d=5(a+2d)
a+15d=5a+10d
4a=5d … (1)
Also,
a₁₀=41
a+9d=41
a=41-9d … (2)
Solving (1) and (2), we get
(1) … 4(41-9d)=5d
164-36d=5d
164=5d+36d
164=41d
d=4
(2) … a=41-9⋅4
=41-36
a=5
Using the formula, S_n=½n[2a+(n-1)d], we get
S₁₅=½⋅15⋅[2⋅5+(15-1)⋅4]
=15⋅½⋅(10+56)
=15⋅33
=495.
Hence, the required sum is 495.
Let’s read an important post Derivation of the partial sum formula of every Arithmetic Series.
P4. The 13th term of an arithmetic sequence is 4 times its 3rd term. If its 5th term is 16 then the sum of its first ten terms is
(a) 150 (b) 175 (c) 160 (d) 135
Solution: Let a be the first term and d be the common difference of the arithmetic sequence. Then,
Given a₁₃=4a₃.
[a_n=a+(n-1)d]
a+12d=4(a+2d)
a+12d=4a+8d
3a=4d … (1).
Given a₅=16
a+4d=16 … (2)
Answer: (b) 175
Solving (1) and (2), we ge
a+3a=16
4a=16
a=4.
Putting a=4 in (1), we get
4d=3⋅4=12
d=3.
Using the formula, S_n=½n[2a+(n-1)d]. we get
S₁₀=½⋅10⋅[2⋅4+(10-1)⋅3]
=5⋅(8+27)
=5⋅35
=175.
Thus, the sum of its first 10 terms is 175.