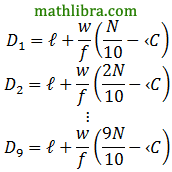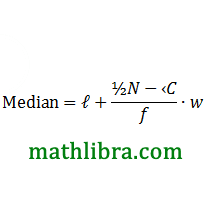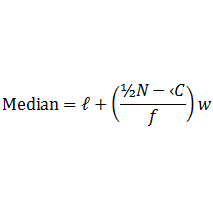Cumulative Histograms
Cumulative histograms, also known as ogives, are a plot of cumulative frequency and are used to determine how many data values lie above or below a particular value in a data set. The cumulative frequency is calculated from a frequency table, by adding each frequency to the total of the frequencies of all data values before it in the data set. The last value for the cumulative frequency will always be equal to the total number of data values, since all frequencies will already have been added to the previous total. The cumulative frequency is plotted at the upper limit of the interval.
What is Cumulative Frequency?
Cumulative is just a posh way of saying “add up as you go along”
Frequency is just a posh word for “total”
So… if you put them together, you get a very posh way of saying “add the totals up as you go along”
Cumulative Frequency Graphs
Sometimes, in addition to finding the median, it is useful to know the number or proportion of scores that lie above or below a particular value. In such situations we can construct a cumulative frequency distribution table and use a graph called a cumulative frequency graph to represent the data.
The cumulative frequencies are plotted and the points joined by a smooth curve. This compares with an ogive or cumulative frequency polygon where two points are joined by straight lines.
For exampe, EXAMPLE 1
The cumulative frequencies for Data Set Ex1 are shown in Table Ex1 and is drawn in Figure Ex1.
Notice the frequencies plotted at the upper limit of the intervals, so the points (30;1) (62;2) (97;3), etc have been plotted. This is different from the frequency polygon where we plot frequencies at the midpoints of the intervals.

Table Ex1: Cumulative Frequencies for Data Set Ex1.

Figure Ex1: Example of a cumulative histogram for Data Set Ex1. Those 6 lines do NOT construct a straight longest line.
Cumulative frequency tables and graphs (ogives)
EXAMPLE 2
In an English class, 30 learners completed a test out of 20 marks. Here is a list of their results:
14 10 11 19 15 11 13 11 9 11 12 17 10 14 13 17 7 14 17 13 13 9 12 16 6 9 11 11 13 20
1. Cumulative frequency tables
● Cumulative frequency gives us a running total of the frequency. So we keep adding onto the frequency from the first interval to the last interval.
● We can show these results in a cumulative frequency table.

With this data set, it would be more useful to group the data.
We can use intervals of 5 and make a cumulative frequency table for grouped data.

2. Cumulative frequency graph (ogive)
● We can represent the cumulative results from a cumulative frequency table with a cumulative frequency graph or ogive.
● This graph always starts on the x-axis and usually forms an S-shaped curve, ending with the cumulative frequency (y-value).
● The endpoint of each interval is plotted against the cumulative frequency.
Represent the data in the cumulative frequency table of grouped data with a cumulative frequency graph.
● the x-axis needs the points 5; l0; l5; and 20 to mark the end of each interval.
● the y-axis represents the cumulative frequency from 0 to 30.
● For plotting the points, use the end of each class interval on the x-axis and the cumulative frequency on the y-axis. So you need to plot these points: (5; 0); (10; 7); (15; 24); (20; 30)
● Join the plotted points.
Hint: To plot ogive:
● x-axis – use upper limit of each interval.
● y-axis – cumulative frequency
● If the frequency of the first interval is not 0, then include an interval before the given one and make use 0 as its frequency.

EXAMPLE 3An ice cream vendor has kept a record of sales for October and November 2018. The daily sales in rands is shown in the histogram below.

(a). Draw up a cumulative frequency table for the sales over October and November.
(b). Draw an ogive for the sales over October and November.
(c). Use your ogive to determine the median value for the daily sales. Explain how you obtain your answer.
(d). Estimate the interval of the upper 25% of the daily sales.
solution:
(a). Cumulative frequency table:

(b).

(c). There are 61 data points, so the median is the 31st data point. We can read the data point off the graph at 31. It gives a rand value of R87.
(d). The upper 25% lies above 75% of 61 is equal to 45.75.
Read from the y-axis across to the graph and down to the x-axis.
The upper 25% of sales lies in the interval: 96≤ sales <120.
EXAMPLE 4To the right is a table showing the length of time a group of 40 Year 10 students spent playing on the Nintendo Wii on a gloomy week n in January. Draw a Cumulative Frequency Curve, use it to estimate the Median and Inter-Quartile Range, and construct a Box Plot

1. Adding a Cumulative Frequency Column
Before you can even start thinking about drawing a Cumulative Frequency Curve, you need to be able to add a Cumulative Frequency column to your Frequency table.
Remember, Cumulative Frequency just means that you add up the frequencies as you go along, so that is exactly what you do!

2. Drawing the Cumulative Frequency Curve
Remember: we plot Cumulative Frequency (y axis) against the upper boundary of each group (x axis)

So… for group one it’s 1 on the x axis and 2 on the y
and for group two, it’s 2 on the x axis and 7 on the y…
Things to notice about the Cumulative Frequency Curve:
(i). When you have finished plotting the points, join them up with a smooth curve.
(ii). Native the curve starts at (0, 0). This is because there is nobody playing less than 0 hours a week!
(iii). You must label your axis correctly, or you lose very easy marks!

3. Estimating the Median and lnter-Quartile Range
We have spent a while drawing our cumulative frequency curve, so we may as well use it. Very quickly we can come up with estimates for the Median and the Inter-Quartile Range
(a) Median
As you hopefully remember, the Median is the MIDDLE value. To find it we:
(i). Work out what is 50% of our total frequency (half way up the y axis)
(ii). Draw a horizontal line across until it hits our curve
(iii). When it hits the curve, draw a vertical line down to the x axis
(iv). The value on the x axis is our Median :

(b) Inter-Quartile Range
For this we need to work out the upper quartile (UQ) and the lower quartile (LQ), and then calculate: UQ- LQ
To find the Upper Quartile:
(i). Work out what is 75% of our total frequency (three-quarters of the way up the y axis)
(ii). Draw a horizontal line across until it hits our curve
(iii). When it hits the curve, draw a vertical line down to the x axis
(iv). The value on the x axis is our Upper Quartile
The Lower Quartile is the same, but 25% (one-quarter) of the way up!

Median: 50% of 40 = 20. Median =3.2 hours
Upper Quatile, 75% of 40 = 30. UQ =3.8 hours
Lower Quatile, 25% of 40 = 10. LQ =2.4 hours
Inter Quatile Range =UQ-LQ=3.8-2.4=1.4 hours
Remember: The Median is a form of average, and just like the Range, the Inter-Quartile Range is a measure of consistency

Why do we bother with Statistical Diagrams?
● The answer to this question is similar to the one for: “why do we bother working out averages and measures of spread?”.
● We live in a world jam-packed full of statistics, and if we were forced to look at all the facts and figures in their raw, untreated form, not only would we probably not be able to make any sense out of them, but there is also a very good chance our heads would explode.
● Statistical Diagrams – if they are done properly – present those figures in a clear, concise, visually pleasing way, allowing us to make some sense out of the figures, summarise them, and compare them to other sets of data.
EXAMPLE 5
The data shows the results of the women’s marathon at the 2008 Olympics, for all competitors who finished the race.

a) Construct a cumulative frequency distribution table.
b) Represent the data on a cumulative frequency graph.
c) Use your graph to estimate the:
i. median finishing time
ii. number of competitors who finished in less than 2 hours 35 minutes
iii. percentage of competitors who took more than 2 hours 39 minutes to finish
iv time taken by a competitor who finished in the top 20% of runners completing the marathon.
solution:
a.

b.

The cumulative frequency gives a progressive total of the number of runners finishing by a given time. It is plotted at the right end boundary of the interval.
c) i. The median is estimated using the 50th percentile. As 50% of 69 is 34.5, we start with the cumulative frequency of 34.5 and find the corresponding time.
The median is approximately 2 hours 34.5 min.
ii. There are approximately 37 competitors who took less than 2h 35 min to complete the race.
iii. There are 69-52=17 competitors who took more than 2 hours 39 min.
So 17/69≈26.4% took more than 2 hours 39 min.
iv. The time taken is estimated using the 20th percentile. As 20% of 69 is 13.8, we find the time corresponding to a cumulative frequency of approximately 14. The top 20% of competitors took less than 2 hours 31 minutes.
EXAMPLE 6
The weights of a random sample of boys in Grade 11 were recorded. The cumu- lative frequency graph (ogive) below represents the recorded weights.
Cumulative frequency curve showing weight of boys

a) How many of the boys weighed between 90 and 100 kilogrammes?
b) Estimate the median weight of the boys.
c) If there were 250 boys in Grade 11, estimate how many of them would weigh less than 80 kilogrammes?
solution:
a) 42-28=14
b) There are 50 boys in total, so the median weight is that of the 〖25〗^th boy. The weight corresponding to a cumulative frequency of 25 is approximately 88 kg.
Note: Accept a range from 86 to 89 kg.
c) 15 boys in the sample have a weight of less than 80 kg. One would expect % x 250=75 boys in the grade to have a weight of less than 80 kg.
EXAMPLE 7
Use the ogive to answer the questions below. Marks give as a percentage (%).

a) How many students got between 50% and 70%?
b) How many students got at least 70%?
c) Compute the average mark for this class, rounded to the nearest integer.
solution:
a) The cumulative plot shows that 15 students got below 50% and 35 students got below 70%. Therefore 35-15=20 students got between 50% and 70%.
b) The cumulative plot shows that 35 students got below 70% and that there are 50 students in total. Therefore 50-35=15 students got at least (greater than or equal to) 70%.
c) To compute the average, we first need to use the ogive to determine the frequency of each interval. The frequency of an interval is the difference between the cumulative counts at the top and bottom of the interval on the ogive. It might be difficult to read the exact cumulative count for some of the points on the ogive. But since the final answer will be rounded to the nearest integer, small errors in the counts will not make a difference. The table below summarises the counts.

The average is then the centre of each interval, weighted by the count in that interval.

The average mark, rounded to the nearest integer, is 60%.
EXAMPLE 8
Draw the histogram corresponding to this ogive.

solution:
To draw the histogram we need to determine the count in each interval.
Firstly, we can find the intervals by looking where the points are plotted on the ogive. Since the points are at x-coordinates of -25; -15; -5; 5; 15 and 25, it means that the intervals are (-25

From these counts we can draw the following histogram:

EXAMPLE 9The following data set lists the ages of 24 people.
2; 5; 1; 76; 34; 23; 65; 22; 63; 45; 53; 38
4; 28; 5; 73; 79; 17; 15; 5; 34; 37; 45; 56Use the data to answer the following questions.
a) Using an interval width of 8 construct a cumulative frequency plot.
b) How many are below 30?
c) How many are below 60?
d) Giving an explanation, state below what value the bottom 50% of the ages fall.
e) Below what value do the bottom 40% fall?
f) Construct a frequency polygon.
solution:
a) The table below shows the number of people in each age bracket of width 8.

From this table we can draw the cumulative frequency plot:

b) 11 people c) 19 people
d) This question is asking for the median of the data set. The median is, by definition, the value below which 50% of the data lie. Since there are 24 values, the median lies between the middle two values, giving 34.
e) There are 24 values. By drawing a number line, as we do for determining quartiles, we can see that the 40% point is between the tenth and eleventh values. The tenth value is 23 and the eleventh value is 28. Therefore 40% of the values lie below (23+28)/2=25.5
f) We already have all the values needed to construct the frequency polygon in the table of values above.

EXAMPLE 10Draw a histogram, frequency polygon and ogive of the following data set. To count the data, use intervals with a width of 1, starting from 0.
0.4;3.1;1.1;2.8;1.5;1.3;2.8;3.1;1.8;1.3;
2.6;3.7;3.3;5.7;3.7;7.4;4.6;2.4;3.5;5.3solution:
We first organise the data into a table using an interval width of 1, showing the count in each interval as well as the cumulative count across intervals.

From the table above we can draw the histogram, frequency polygon and ogive.