Different Types of Linear Programming Problems

A few important linear programming problems are listed below:
1. Manufacturing problems. In these problems, we determine the number of units of different products which should be produced and sold by a firm when each product requires a fixed manpower, machine hours, labour hour per unit of product, warehouse space per unit of the output etc., in order to make maximum profit.
2. Diet problems.
3. Transportation problems.

📌 Example 1 (Manufacturing problem).

A manufacturing company makes two models A and B of a product. Each piece of Model A requires 9 labour hours for fabricating and 1 labour hour for finishing. Each piece of Model B requires 12 labour hours for fabricating and 3 labour hours for finishing. For fabricating and finishing, the maximum labour hours available are 180 and 30 respectively. The company makes a profit of USD8000 on each piece of model A and USD12000 on each piece of Model B. How many pieces of Model A and Model B should be manufactured per week to realise a maximum profit? What is the maximum profit per week?

✍ Solution:
Suppose x is the number of pieces of Model A and y is the number of pieces of Model B. Then

Total profit (in USD)=8000x+12000y
Let Z=8000x+12000y
We now have the following mathematical model for the given problem.
Maximise Z=8000x+12000y…(1)
subject to the constraints:
9x+12y≤180…(÷3) (Fabricating constraint)
3x+4y≤60…(2)
x+3y≤30…(3) (Finishing constraint)
x≥0, y≥0…(4) (non—negative constraint)

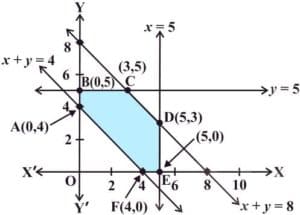
The feasible region (shaded) OABC determined by the linear inequalities (2) to (4) is shown in the Fig 1. Note that the feasible region is bounded.

[Fig 1]
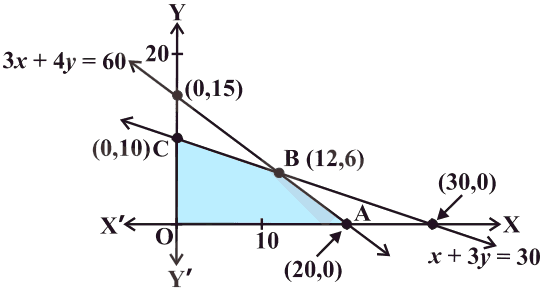
Let us evaluate the objective function Z at each corner point as shown below:

Corner Point	Z=8000x+12000y
O (0, 0) A (20, 0) B (12, 6) C (0, 10)	0 160000 168000 ← Maximum 120000

We find that maximum value of Z is 1,68,000 at B (12, 6). Hence, the company should produce 12 pieces of Model A and 6 pieces of Model B to realise maximum profit and maximum profit then will be USD168,000.

📌 Example 2 (Manufacturing problem).
A manufacturer has three machines I, II and III installed in his factory. Machines I and II are capable of being operated for at most 12 hours whereas machine III must be operated for atleast 5 hours a day. She produces only two items M and N each requiring the use of all the three machines.

The number of hours required for producing 1 unit of each of M and N on the three machines are given in the following table:

Items	Number of hours required on machines
	I	II	III
M	1	2	1
N	2	1	1.25

She makes a profit of USD600 and USD400 on items M and N respectively. How many of each item should she produce so as to maximise her profit assuming that she can sell all the items that she produced? What will be the maximum profit?
✍ Solution:
Let x and y be the number of items M and N respectively.
Total profit on the production=USD(600x+400y).
Mathematical formulation of the given problem is as follows:
Maximise Z=600x+400y
subject to the constraints:

x+2y≤12…(1) (constraint on Machine I)
2x+y≤12…(2) (constraint on Machine II)
x+5y/4≥5…(3) (constraint on Machine III)
x≥0, y≥0…(4)
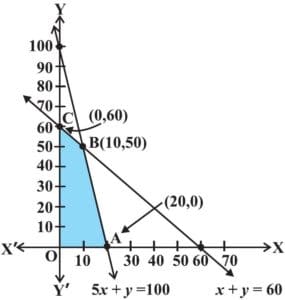
Let us draw the graph of constraints (1) to (4). ABCDE is the feasible region (shaded) as shown in [Fig 2] determined by the constraints (1) to (4). Observe that the feasible region is bounded, coordinates of the corner points A, B, C, D and E are (5, 0) (6, 0), (4, 4), (0, 6) and (0, 4) respectively.

[Fig 2]
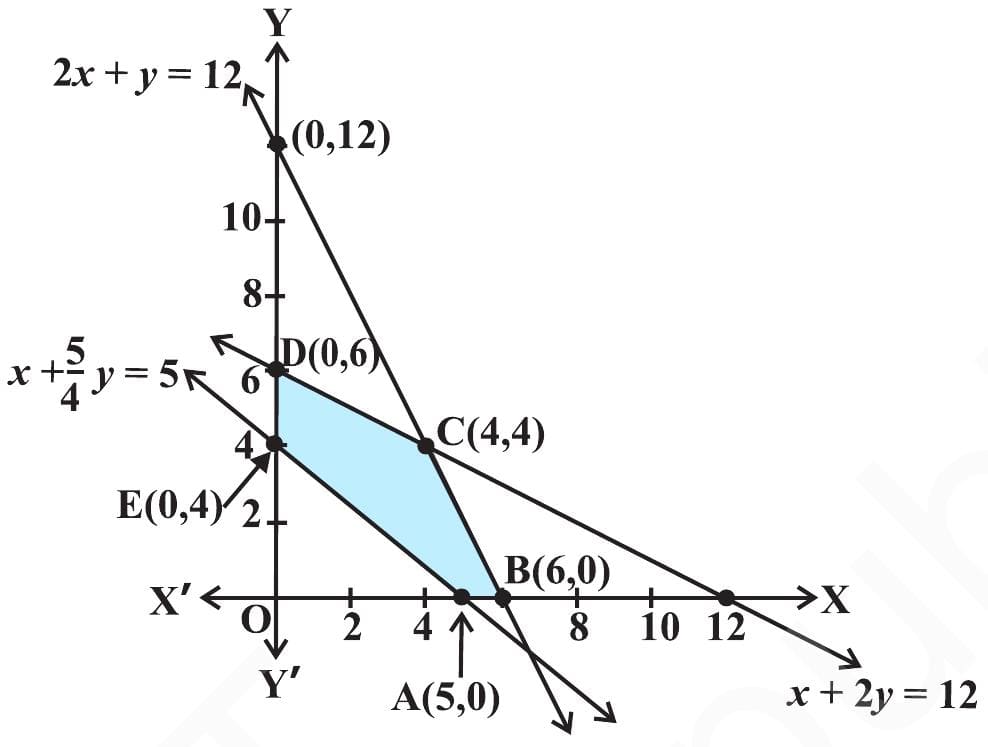
Let us evaluate Z=600x+400y at these corner points.

Corner Point	Z=600x+400y
(5, 0) (6, 0) (4, 4) (0, 6) (0, 4)	3000 3600 4000 ← Maximum 2400 1600

We see that the point (4, 4) is giving the maximum value of Z. Hence, the manufacturer has to produce 4 units of each item to get the maximum profit of USD4000.

📌 Ex3. A certain motorcycle manufacturer produces two basic models, the Super X and the Super Y. These motorcycles are sold to dealers at a profit of $20,000 per Super X and $10,000 per Super Y. A Super X requires 150 hours for assembly, 50 hours for painting and finishing and 10 hours for checking and testing. The Super Y requires 60 hours for assembly, 40 hours for painting and finishing and 20 hours for checking and testing. The total number of hours available per month is: 30,000 in the assembly department, 13,000 in the painting and finishing de- partment and 5,000 in the checking and testing department.

The above information is summarised by the following table:

Department	Hours for Super X	Hours for Super Y	Hours available per month
Assembly	150	60	30,000
Painting and finishing	50	40	13,000
Checking and testing	10	20	5,000

Let x be the number of Super X and y be the number of Super Y models manu- factured per month.
a) Write down the set of constraint inequalities.
b) Use graph paper to represent the set of constraint inequalities. c) Shade the feasible region on the graph paper.
d) Write down the profit generated in terms of x and y.
e) How many motorcycles of each model must be produced in order to maximise the monthly profit?
f) What is the maximum monthly profit?
✍ Solution:
a) Adding the assembly hours:

150x+60y≥30,000
Adding the painting and finishing:
50x+40y≥13,000
Adding the checking and testing:
10x+20y≥5,000
b)

c) See above
d)
E=(profit per Super X)×(number of Super X bikes sold)
+(profit per Super Y) × (number of Super Y bikes sold)
E=(20,000)x+(10,000)y
e) The vertices of the feasible region are as follows:
Point A: (0; 0)
Point B: (200; 0)
Point C: (140; 150)
Point D: (100; 200)
Point E: (0; 250)
The cost at each vertex is as follows:
Point A: E=20,000(0)+10,000(0)=0
Point B: E=20,000(200)+10,000(0)=4,000,000
Point C: E=20,000(140)+10,000(150)=4,300,000
Point D: E=20,000(100)+10,000(200)=4,000,000
Point E: E=20,000(0)+10,000(250)=2,500,000
To maximize the objective function select Point C.
The maximum profit can be made if 140 Super X motorbikes and 150 Super Y motorbikes are sold.
f) The maximum possible profit is $4,300,000.
Let you read pages
💎 Diet Problems, also
🎲 Linear Programming Keywords: company, factory, manufacture, maximize, maximum, profit.