Disjoint sets

Two sets are disjoint if they have no elements in common, i.e., if their intersection is the empty set.

⛲ Example 1. Is there a disjoint pair from among C={1,2,3,4}, D={2,4,6,8} and E={3,5,7,9}?
• D∩E=Ø, so D and E are disjoint.
C and D have elements in Common, so they are not disjoint. Also, C and E are not disjoint.

Disjoint sets

Two sets are called disjoint if they have no elements in common. For example:

The sets S={2,4,6,8} and T={1,3,5,7} are disjoint.

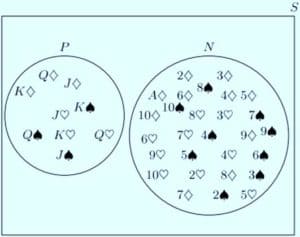
Another way to define disjoint sets is to say that their intersection is the empty set. Two sets A and B are disjoint if A∩B=Ø.
In the example above,
S∩T=Ø because no number lies in both sets.

Representing disjoint sets on a Venn diagram

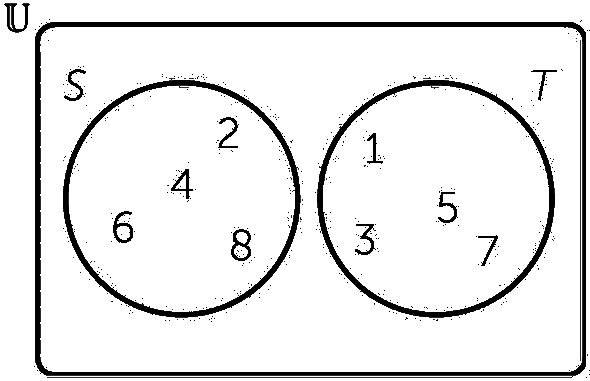
When we know that two sets are disjoint,we represent them by circles that do not intersect. For example,let

P={0,1,2,3} and Q={8,9,10}
Then P and Q are disjoint,as illustrated in the Venn diagram below.

[Definition] Two sets are said to be disjoint if they have no element in common.

⛲ Ex2. The sets, F={0,4,7,9} and G={3,6,10} are disjoint.

⛲ Ex3. State whether each of the following statement is true or false. Justify your answer.
(i) {2,3,4,5} and {3,6} are disjoint sets.
(ii) {a,e,i,o,u } and {a,b,c,d} are disjoint sets.
(iii) {2,6,10,14} and {3,7,11,15} are disjoint sets.
(iv) {2,6,10} and {3,7,11} are disjoint sets.
✍ Solution:
(i) False
As 3∈{2,3,4,5}, 3∈{3,6}
⇒{2,3,4,5}∩{3,6}={3}
(ii) False
As a∈{a,e,i,0,u}, a∈{a,b,c,d}
⇒{a,e,i,o,u}∩{a,b,c,d}={a}
(iii) True
As {2,6,10,14}∩{3,7,11,15}=Ø
(iv) True
As {2,6,10}∩{3,7,11}=Ø

⛲ Ex4. State whether each of the following statement is true or false.
(i) H={2,4,6,8} and I={1,3,5} are disjoint sets.
(ii) J={a,e,i,o,u} and K={a,b,c,d} are disjoint sets.
✍ Solution:
(i) We have,H={2,4,6,8} and I={1,3,5}
Now, H∩I={2,4,6,8}∩{1,3,5}=Ø.
Therefore, H and I are disjoint sets. Hence, given statement is true.
(ii) We have, J={a,e,i,o,u} and K={a,b,c,d} Now, J∩K={a}. ∴ J∩K≠Ø.
Therefore, J and K are not disjoint sets. Hence, given statement is false.

⛲ Ex5. Which of the following pairs of sets are disjoint
(i) {1,2,3,4} and {x:x is a natural number and 4≤x≤6}
(ii) {a,e,i,o,u} and {c,d,e,f}
(iii) {x:x is an even integer} and {x:x is an odd integer}
✍ Solution:
(i) {1,2,3,4}
{x:x is a natural number and 4≤x≤6}={4,5,6}.
Now, {1,2,3,4}∩{4,5,6}={4}
Therefore,this pair of sets is not disjoint.
(ii) {a,e,i,o,u}∩(c,d,e,f}={e}
Therefore, {a,e,i,o,u} and (c,d,e,f} are not disjoint.
(iii) {x:x is an even integer}∩{x:x is an odd integer}=Ø
Therefore, this pair of sets is disjoint.

⛲ Ex6. Which of the following pairs of sets are disjoint?
(i) L={1,2,3,4,5,6} and M={x:x is a natural number and 4≤x≤6}
(ii) N={x:x is the boys of your school}, O={x:x is the girls of your school}
🌟 Firstly, convert all the sets in roster form, if it is not given in that. Then use the condition for disjoint sets i.e., A∩B=Ø.
✍ Solution:
(i) Given, L={1,2,3,4,5,6} and M={4,5,6}
∴ L∩M={1,2,3,4,5,6}∩{4,5,6}={4,5,6}≠Ø
Hence, this pair of sets is not disjoint.
(ii) Here, N={b₁,b₂,…} and O={g₁,g₂,…},
where b₁,b₂,…, are the boys and g₁,g₂,…, are the girls of school.
Clearly, N∩O=Ø
Hence, this pair of set is disjoint set.