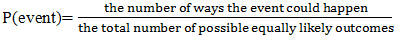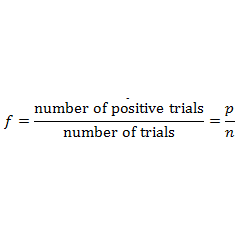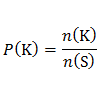In broadcast news, Several TV programs often broadcast weather forecasts, which are often called the weather estimation, for example: New York is rain, Los Angeles is sunny and other. In weather forecast, the statement that New York is rain, is an event that is estimated to occur. The estimation is based on analysis of data related to the occurence of rain. And in the analysis that the probability of the occurence of rain is greater than not rain, so is concluded that New York is rain. Various events can be estimated or guessed, for example, in the final European Club soccer match in 2016, I estimate the italy could beat France, but in fact France won and become champion. It means that my estimation is not percisely.
In any research or experiments that contain uncertainly, we need to draw a conclusion. In order to estimate the conclusion accurately then we need to understand the theory of probability.
A coin has two sides, suppose we call the number side (N) for the first side and we call the image side (E) for the second side. If a coin we spin, then after the coin stops spinning , one side will be facing up so that we can read. In spinning this coin we can see the fact: the number (N) is readable or the image (E) is readable. The number side is readable is the one event and the image side is readable is also one event.

The union of events the number side read and the image side read is called the sample space.
The sample space is the set of all possible outcome of some given experiment. Sample space is generally denoted by S. Each member of the sample space is called the sample point. Event is a subset of the sample space.
Example 1:
a. Suppose a die is tossed. If S is the sample space of the top side is readable, detemine S and many members of S. If X states the event that the top side which is readable is an even number, determine the X and many members of X.
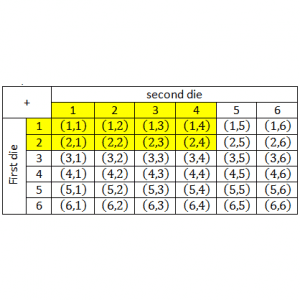
b. suppose two dice are tossed together. If S is the sample space of the emergence of the eye of dice from these two dice, determine S and many members of S. If K states an events that the eye dice which appear are same, determine K and many members of K.
Answer:
a. Sample space is: S={1,2,3,4,5,6}.
The the number of elements of S is: n(S)=6.
X=The event that top side readable are even number.
→X={2,4,6}. The the number of elements of X is: n(X)=3.
b.
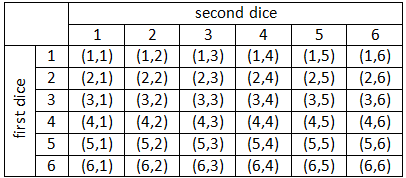
S={(1,1), (1,2), (1,3), (1,4), (1,5), (1,6), (2,1), (2,2), (2,3), (2,4), (2,5), (2,6), (3,1), (3,2), (3,3), (3,4), (3,5), (3,6), (4,1), (4,2), (4,3), (4,4), (4,5), (4,6), (5,1), (5,2), (5,3), (5,4), (5,5), (5,6), (6,1), (6,2), (6,3), (6,4), (6,5), (6,6)}.
The the number of elements of S is: n(S)=36=62.
K=The event that the eye dice which appear are some.
→X={(1,1), (2,2), (3,3), (4,4), (5,5), (6,6)}
The the number of elements of K is: n(K)=6.
1. In coin tossing experiment, suppose N states the number side is appeared (readable) and E states the image side is appeared. If the two coins are tossed together, determine the sample space of the emergence of coins side. Calculate the the number of elements of the sample space.
Answer:

Four members.
2. For experiment of tossing one coin and one die at the same time, determine the sample space that is appeared (the top side is readable) of the result of the tossing. Calculate the the number of elements of the sample space. If K is event that appears is the number side of the coin and the prime numbers of the die, determine K and the the number of elements of the K.
Answer:
Suppose the coin has two sides and the die has six sides. Thus, The sample space (S) contains:
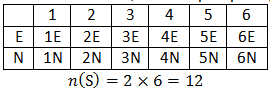
The number side of coin is (N). And the prime numbers of the die are {2,3,5}
Answer:
Each coin has two sides. The the number of elements of the sample space 2×2×2=23=8.
Members of K are arranged by two (N) and one (E). K={NNE,NEN,ENN}→n(K)=3
4. In a bag, there are three marbles with different color. If two marbles are taken at the same time, determine the sample space of the result of taking. How many members of the sample space.
Answer:
There is no sequence. Use combination
Answer: