For any natural number n, we define factorial as n! or
And 0!=1!=1
n factorial
:
The continuous product of the first n natural numbers is called factorial n and is denoted by n!.
Addition Principle between Multiplication and Factorial
:
Consider the 3 letter words starting or finishing with O that can be made from the letters WORD if no letter is repeated. Now words starting or finishing with O are mutually exclusive i.e., they do not overlap.
Therefore we can find the number starting with O and the number finishing with O and add the two numbers.
Starting with O:
| Letter I | Letter II | Letter III | Num of words |
|---|---|---|---|
| 1× | 3× | 2× | =6 |
Finishing with O:
| Letter I | Letter II | Letter III | Num of words |
|---|---|---|---|
| 3× | 2× | 1× | =6 |
Number of words starting or finishing with 0 =6+6=12.
This is an illustration of the addition principle i.e., if two operations are mutually exclusive (i.e. they do
not overlap), then the number of ways of performing one operation or the other is the sum of the numbers of ways of performing each operation.
If an operation can be performed in m different ways and another operation in n different ways then either of these two operations can be performed in m+n ways. (Provided only one has to be done)
This principle can be extended to any number of operations.
Q1: Given the word: EDUCATION
12.1. In how many unique ways can all the letters in the word above be arranged?
12.2. If 5 letters are randomly chosen from the word ‘EDUCATION’. determine how many unique 5-letter arrangements can be formulated?
Solutions:
12.1. 9!=362880 (any other valid representation of the answer).
12.2. 9∙8∙7∙6∙5=(9∙8∙7∙6∙5∙4!)/4!=9!/(9-5)!=15120
Q2:
The letters of the word DECIMAL are randomly arranged into a new ‘word’, also consisting of seven letters. How many different arrangements are possible if:
(i). Letters may be repeated
(ii). Letters may not be repeated
(iii). The arrangements must start with a vowel and end in a consonant and no repetition of letters is allowed
Solutions:
(i). 77=823543
(ii). 7!=5040
(iii). There are 3 vowels ⇒ 3 options for first position
There are 4 consonants ⇒ 4 options for last position
The remaining 5 letters can be arranged in 5×4×3×2×1 ways. Hence, Hence, number of different arrangements
=3×(5×4×3×2×1)×4=1440
Q3. In how many different ways can we arrange 7 books on a shelf?
Solution:
7!=5040 different ways 7 books can be arranged on a shelf.
Q4. In how many different ways can 9 girls sit on one side of a table?
Solution:
9!=362880 different ways for 9 girls to sit on one side of a table. 11
Q5. How many words can be formed from the letters of the following words using all letters when no letter is to be repeated?
(i). PLANE
Solution:
Here n=5
The number of words formed by the letters of word “PLANE” is 5!=5∙4∙3∙2∙1=120
(ii). OBJECT
Solution:
Here n=6
The number of words formed by the letters of word “OBJECT” is 6!=6∙5∙4∙3∙2∙1 =720
(iii) FASTING
Solution:
Here n=7
The number of words formed by the letters of word “FASTING” is 7!=7∙6∙5∙4∙3∙2∙1=5040
Q6:
Find the number of arrangements of 3 books on English and 5 books on Urdu for placing them on a shelf such that the books on the same subject are together?
Solution:
E1E2E3U1U2U3U4U5→=3!×5!=6×120=720
Arrangement of books of the form
U1U2U3U4U5E1E2E3→=3!×5!=6×120=720
Total arrangements =720+720=1440
Q7:
Consider the word MATHS.
(i). How many different 5-letter arrangements can be made using all the above letters?
(ii). Determine the probability that the letters S and T will always be the first two letters.
Solutions:
(i). Number of different letters arrangements:
| Letter I | II | III | IV | V |
|---|---|---|---|---|
| 5× | (5-1)× | (5-2)× | (5-3)× | (5-4)× |
Number of different letter arrangements:
(ii). S and T can be arranged in 2! different ways.
The remaining three letters can be arranged in 3! different ways.
∴ Total number of different letter arrangements having S and T as the first two letters =2!∙3!=2×6=12
P(having S and T as first two letters)
Q8. In how many ways can 5 boys and 4 girls be seated on a bench so that the girls & boys occupy alternate seats?
Solution:
Let B1B2,…,B5denote the numbers of boys and
G1G2,…,G4denote the numbers of girls.
Required arrangement
=5!×4!
=5∙4∙4∙3∙3∙2∙2∙1∙1=2880
Q9:
It is required to seat 5 men and 4 women in a row so that the women occupy the even places. How many such arrangements are possible?
Solution:
4 men and 4 women are to be seated in a row such that the women occupy the even places.
M1W1M2W2M3W3M4W4M5
The 5 men can be seated in 5! Ways. For each arrangement, the 4 women can be seated only at
the cross marked places (so that women occupy the even places).
Therefore, then women can be seated in 4! ways.
Thus, possible number of arrangements
Q10. Find the number of ways in which five different books can be put on a shelf one over the other such that English book is above the Latin book?
A. 120 B.60 C. 24 D.48
correct: B, solution:
Five books can be arranged in 5! ways.
Half the times the English book is above the Latin book and half the times Latin book is above the english book.
So, total number of ways in which the books can be arranged =5!/2=60 ways.
Q11:
How many 6-digit numbers can be formed from the digits, 0, 1, 3, 5, 7 and 9 which are divisible
by 10 and no digit is repeated?
Solution:
A number is divisible by l0 if its units digits is 0.
Therefore, 0 is fixed at the units place.
Therefore, there will be as many ways as there are ways of filling 5 vacant places [_][_][_][_][_][0]
in succession by the remaining 5 digits (i.e., 1, 3, 5, 7 and 9).
The 5 vacant places can be filled in 5! Ways.
Hence, required number of 6-digit numbers =5!=120
Q12:
The digits 1 to 7 are used to create a four -digit code to enter a locked room. How many different codes are possible if the digits may not be repeated and the code must be an even number bigger than 5000?
Solution:
We want to create codes that are even numbers greater than 5000. The digit 6 can be used in one of two places in these codes and therefore this presents two scenarios.
Case 1: The first digit is a 6.
| 6 | {2,4} |
Number of codes starting with 6.
Case 2: The first digit is a 5 or 7.
| {5,7} | {2,4,6} |
Number of codes not starting with 6.
Therefore total number of possible codes =40+120=160.
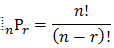
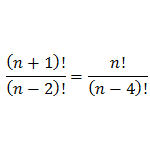
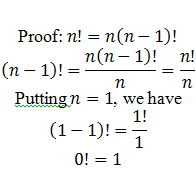
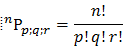

1 comment on factorial