Question 1: Suppose we wish to arrange n=5 people {a,b,c,d,e}, standing side by side, for a portrait. How many such distinct portraits (“permutations”) are possible?
Example:
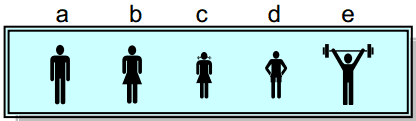
Here, every different ordering counts as a distinct permutation. For instance, the ordering (a,b,c,d,e) is distinct from (c,e,a,d,b), etc.
Solution: There are 5 possible choices for which person stands in the first position (either a, b, c, d, or e). For each of these five possibilities, there are 4 possible choices left for who is in the next position. For each of these four possibilities, there are 3 possible choices left for the next position, and so on. Therefore, there are 5×4×3×2×1=120 distinct pennutations. See Table 1.
This number, 5×4×3×2×1 (or equivalently, 1×2×3×4×5), is denoted by the symbol “5!” and read “5 factorial”, so we can write the answer succinctly as 5!=120.
In general,
FACT 1: The number of distinct PERMUTATIONS of n objects is “n factorial”, denoted by
n!=1×2×3×…×n, or equivalently,
=n(n-1)(n-2)×…×2×1
Example:
6!=6×5×4×3×2×1
6!=6×5!=720
Question 2: Now suppose we start with the same n=5 people {a,b,c,d,e}, but we wish to make portraits of only k=3 of them at a time. How many such distinct portraits are possible?
Example:

Again, as above every different ordering counts as a distinct permutation. For instance, the ordering (a,b,c) is distinct from (c,a,b), etc.
Solution: By using exactly the same reasoning as before, there are 5×4×3=60 permutations.
See Table 2 for the explicit list!
Note that this is technically NOT considered a factorial (since we don’t go all the way down to l), but we can express it as a ratio of factorials:

In general,
FACT 2: The number of distinct PERMUTATIONS of n objects, taken k at a time, is given by the ratio

Question 3: Finally suppose that instead of portraits (“permutations”), we wish to form committees (“combinations”) of k=3 people from the original n=5. How many such distinct committees are possible?
Example:

Now, every different ordering does NOT count as a distinct combination. For instance, the committee {a,b,c} is the same as the committee {c,a,b}, etc.
Solution: This time the reasoning is a little subtler. From the previous calculation, we know that
# of permutations of k=3 from n=5 is equal to 5!/2!=60.
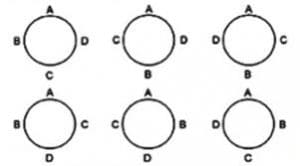
But now, all the ordered permutations of any three people (and there are 3!=6 of them, by FACT 1), will “collapse” into one single unordered combination, e.g., {a,b,c}, as illustrated. So…
# of combinations of k=3 from n=5 is equal to 5!/2! , divided by 3!, i.e., 60÷6=10. See Table 3 for the explicit list!
This number, 5!/3!2!, is given the compact notation 5C3, read “5 choose 3”, and corresponds to the number of ways of selecting 3 objects from 5 objects, regardless of their order. Hence

In general,
FACT 3: The number of distinct COMBINATIONS of n objects, taken k at a time, is given by the ratio

This quantity is usually written as nCk and read “n choose k”.
Examples:








Observe that it is neither necessary nor advisable to compute the factorials of large numbers directly. For instance, 8!=40320, but by writing it instead as 8×7×6!, we can cancel 6!, leaving only 8×7 above. Likewise, 14! cancels out of 15!, leaving only 15, so we avoid having to compute 15!, etc.
Remark:




Exercise: List all the ways of choosing 2 objects from 5, say a,b,c,d,e, and check these claims explicitly. That is, match each pair with its complementary triple in the list of Table 3.
Suppose you toss a coin n=5 times in a row. How many ways can you end up with k=3 heads?
Solution: The answer can be obtained by calculating the number of ways of rearranging 3 objects among 5; it only remains to determine whether we need to use permutations or combinations. Suppose, for example, that the 3 heads occur in the first three tosses, say a, b, and c, as shown below. Clearly, rearranging these three letters in a different order would not result in a different outcome. Therefore, different orderings of the letters a, b, and 0 should not count as distinct permutations, and likewise for any other choice of three letters among a,b,c,d,e. Hence, there are

Exercise: Let “H” denote heads, and “T” denote tails. Using these symbols, construct the explicit list of 10 combinations. (Suggestion: Arrange this list of H/T sequences in alphabetical order. You should see that in each case, the three H positions match up exactly with each ordered triple in the list of Table 3. Why?)

Table 1 — Permutations of {a,b,c,d,e}
These are the 5!=120 ways of arranging 5 objects, in such a way that all the different orders count as being distinct.

Table 2 — Permutations of {a,b,c,d,e}, taken 3 at a time
These are the 5!/2!=60 ways of arranging 3 objects among 5, in such a way that different orders of any triple count as being distinct, e.g., the 3!=6 permutations of (a,b,c), shown below.

Table 3 — Combinations of {a,b,c,d,e}, taken 3 at a time
If different orders of the same triple are not counted as being distinct, then their six permutations are lumped as one, e.g., {a,b,c,}. Therefore, the total number of combinations is ⅙ of the original 60, or 10. Notationally, we express this as 1/3! of the original 5!/2!, i.e., 5!/3!2!, or more neatly, as



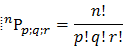


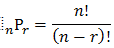
1 comment on Find Difference Between Permutations and Combinations With The Best Summary