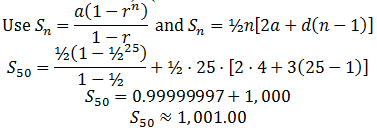Problem 1. If the sum of the first n terms of an arithmetic sequence is given by S_n=2n²+5n, Find the nth term of the arithmetic sequence
Solution: We shall use the formula

a_n=S_n–S_(n-1); n=2,3,4, … ; a₁=S₁
Where S₀=0
∴ a_n=2n²+5n-[2(n-1)²+5(n-1)]
=2n²+5n-[2(n²-2n+1)+5n-5]
=2n²+5n-2n²+4n-2-5n+5
a_n=4n+3
Thus, nth term of the arithmetic sequence is 4n+3.

P2. The sum of first n terms of an arithmetic sequence is (5n–n²) The nth term of the arithmetic sequence is
(a) (5-2n) (b) (6-2n) (c) (2n-5) (d) (2n-6)
Sol:
Let S_n denotes the sum of first n terms of the arithmetic sequence.

S_n=5n–n²
S_(n-1)=5(n-1)-⋅(n-1)²=5n-5-n²+2n-1
=7n–n²-6
∴ nth term of the arithmetic sequence, a_n=S_n–S_(n-1)
=(5n–n²)-(7n–n²-6)
=6-2n
Thus, the nth term of the arithmetic sequence is (6-2n).
Answer: (b) (6-2n)

P3. The sum of the first it terms of an arithmetic sequence is (4n²+2n). The nth term of this arithmetic sequence is
(a) (6n-2) (b) (7n-3) (c) (8n-2) (d) (8n+2)
Solution:
Let S_n denotes the sum of first n terms of the arithmetic sequence.

S_n=4n²+2n
⇒S_(n-1)=4⋅(n-1)²+2(n-1)
=4(n²-2n+1)+2(n-1)
=4n²-6n+2
∴ nth term of the arithmetic sequence, a_n=S_n–S_(n-1)
=(4n²+2n)-(4n²-6n+2)
=8n-2
Thus, the nth term of thee arithmetic sequence is (8n-2)
Answer: (c) (8n-2)

P4. If the sum of n terms of an arithmetic sequence is 2n+3n². Find the nth term.
Solution:
We have S_n=2n+3n²

S_(n-1)=2(n-1)+3(n-1)²
=2(n-1)+3(n²-2n+1)
=2n-2+3n²-6n+3
S_(n-1)=3n²-4n+1
nth term =a_n=S_n–S_(n-1)
=2n+3n²-(3n²-4n+1)
=2n+3n²-3n²+4n-1
a_n=6n-1

P5. The sum of the first n terms of an arithmetic sequence is (3n²+6n). Find the nth term and the 15th term of this arithmetic sequence.
Solution:
Let S_n denotes the sum of first n terms of the arithmetic sequence.

S_n=3n²+6n
S_(n-1)=3(n-1)²+6(n-1)
=3(n²-2n+1)+6(n-1)
=3n²-3
∴ nth term of the arithmetic sequence, a_n.
=S_n–S_(n-1)
=(3n²+6n)-(3n²-3)
=6n+3
Putting n=15, we get a₁₅=6⋅15+3=90+3=93
Hence, the nth term is (6n+3) and 15th term is 93.

P6. The sum of the first n terms of an arithmetic sequence is given by S_n=(3n²–n). Find its
(i) nth term, (ii) first term and (iii) common difference.
Solution:
Given S_n=(3n²–n) … (a)
Replacing n by (n-1) in (a), we get:

S_(n-1)=3(n-1)²-(n-1)
=3(n²-2n+1)-n+1
=3n²-7n+4
(i) Now, a_n=S_n–S_(n-1)
=(3n²–n)-(3n²-7n+4)=6n-4
∴ nth term, a_n=(6n-4) … (b)
(ii) Putting n=1 in (b), we get:
a₁=(6⋅1)-4=2
(iii) Putting n=2 in (b), we get:
a₂=(6⋅2)-4=8
∴ Common difference, d=a₂–a₁=8-2=6

P7. If the sum of first in terms of an arithmetic sequence is (2m²+3m) then what is its second term? Solution:
Let S_m denotes the sum of first In terms of the arithmetic sequence.

∴ S_m=2m²+3m
=2⋅(m-1)²+3(m-1)=2(m²-2m+1)+3(m-1)=2m²–m-1
Now,
mth term of arithmetic sequence, a_m=S_m–S_(m-1)
∴ a_m=2m²+3m-(2m²–m-1)
a_m=4m+1
Putting m=2, we get
a₂=4⋅2+1=9
Hence, the second term of the arithmetic sequence is 9.

P8. The sum of n terms is given by S_n=½n(1+n). Determine a₅.
Solution:

S₅=½⋅5⋅(1+5)=15
S₄=½⋅4⋅(1+4)=10
a₅=15-10=5

P9. (Prizes) A radio station is offering a total of $8500 in prizes over ten hours. Each hour, the prize will increase by $100. Find the amounts of the first and last prize.
Solution:
Given n=10, d=100 and S₁₀=8500.
Find the value of a₁.

S_n=½n[2a₁+(n-1)d]
S₁₀=½⋅10⋅[2a₁+(10-1)100]
8500=5⋅[2a₁+900]
a₁=400
Find the value of a₁₀.
a₁₀=a₁+(n-1)d
=400+(10-1)100
=1300
Answer: $400 and $1300

P10. In an AP: given a₃=15, S₁₀=125, find d and a₁₀.
Solution:
Here, a₃=15 and S₁₀=125.

a₃=15
a+(3-1)d=15
a+2d=15
a=15-2d … (1)
The sum of n terms of an arithmetic sequence is given by
S_n=½n[2a+(n-1)d]
S₁₀=½⋅10⋅[2a+(10-1)d]
125=5[2a+9d]
2a+9d=25
Putting the value of a from equation (1), we get
2(15-2d)+9d=25
30-4d+9d=25
5d=-5
d=-1
Putting the value of d in equation (1), we get
a=15-2(-1)=17
a_n=a+(n-1)d
a₁₀=17+(10-1)(-1)= 17-9 =8
a₁₀=8

P11. In an AP: given d=5, S₉=75, find a and a₉.
Solution:
Here, d=5 and S₉=75. The sum of n terms of an arithmetic sequence is given by

S_n=½n[2a+(n-1)d]
S₉=½⋅9⋅[2a+(9-1)(5)]
75=½⋅9⋅[2a+40]
75=9a+180
75-180=9a
a=-105/9=-35/3=-11⅔
⇒a_n=a+(n-1)d
a₉=-11⅔+(9-1)5
a₉=-11-⅔+40
a₉=40-11-⅔
a₉=28⅓

P12. If the sum of a certain number of terms of the arithmetic sequence 25, 22, 19, is 116. Find the last term
Solution:
Let the sum of n terms of the given arithmetic sequence be 116.

S_n=½n[2a+(n-1)d]
Here, a=25 and d=22-25=-3
116=½n[2⋅25+(n-1)(-3)]
232=n⋅[50-3n+3]
232=53n-3n²
3n²-53n-232=0
3n²-24n-29n+232=0
3n(n-8)-29(n-8)=0
(n-8)(3n-29)=0
n=8 or n=29/3
However, n cannot be equal to 29/3. Therefore, n=8. ∴ The last term
a₈=a₁+d(8-1)
a₈=25-3⋅7=4
Thus, the last term of the arithmetic sequence is 4.

P13. The sum of the first eight terms of an arithmetic sequence {a_n} is 24; the sixth term is 0. Find a formula for a_n.
Solution:
For a_n, first find a and d. Since: a₆=a+5d,a+5d=0. Express S₈ in terms of a and d,

S₈=½⋅8⋅[a+(a+7d)]=4(2a+7d)
Since we are given S₈=24, Equation (3) states that 4(2a+7d)=24. This gives a pair of equations to solve for a and d.

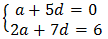
We find d=-2 and a=10. Therefore, the nth term is
a_n=a+(n-1)d=10+(n-1)(-2)=12-2n.

P14. In an arithmetic sequence, the first term is 2 and the sum of the first five terms is one-fourth of the next five terms. Show that 20th term is -112.
Solution:
First term =2
Let d be the common difference of the arithmetic sequence
Therefore, the arithmetic sequence is 2, 2+d, 2+2d, 2+3d,
Sum of first five terms =10+10d
Sum of next five terms =10+35d
According to the given condition,

10+10d=¼(10+35d)
40+40d=10+35d
30=-5d
d=-6
a₂₀=a+(20-1)d=2+(19)(-6)=2-114=-112
Thus, the 20th term of the arithmetic sequence is -112.

P15. The sum of the first 14 terms of and arithmetic sequence is 1505 and its first term is 10. Find its 25th term.
Solution:
Let d be the common difference of the arithmetic sequence.
Here, a=10 and n=14.
Given S₁₄=1505.

S_n=½n[2a+(n-1)d]
½⋅14⋅[2⋅10+(14-1)⋅d]=1505
7(20+13d)=1505
20+13d=215
13d=215-20=195
d=15
∴ 25th term of the arithmetic sequence,
a₂₅=10+(25 -1)⋅15
=10+360
=370.
Hence, the required term is 370.