Solved Problem 1.
Holiday Meal Turkey Ranch is considering buying two different types of turkey feed. Each feed contains, in varying proportions, some or all of the three nutritional ingredients essential for fattening turkeys.
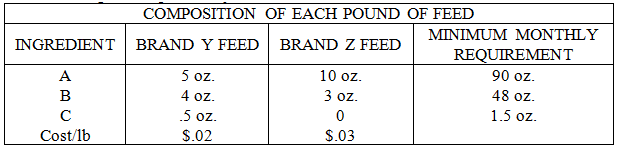
Brand Y feed costs the ranch $.02 per pound. Brand Z costs $.03 per pound. The rancher would like to determine the lowest-cost diet that meets the minimum monthly intake requirement for each nutritional ingredient.

The following table contains relevant information about the composition of brand Y and brand Z feeds, as well as the minimum monthly requirement for each nutritional ingredient per turkey.

SOLUTION
If we let
X₁= number of pounds of brand Y feed purchased
X₂= number of pounds of brand Z feed purchased
then we may proceed to formulate this linear programming problem as follows:
Minimize cost (in cents) =2X₁+3X₂
subject to these constraints:
5X₁+10X₂≥90 oz. (ingredient A constraint)
4X₁+3X₂≥48 oz. (ingredient B constraint)
½X₁≥1½ oz. (ingredient C constraint)

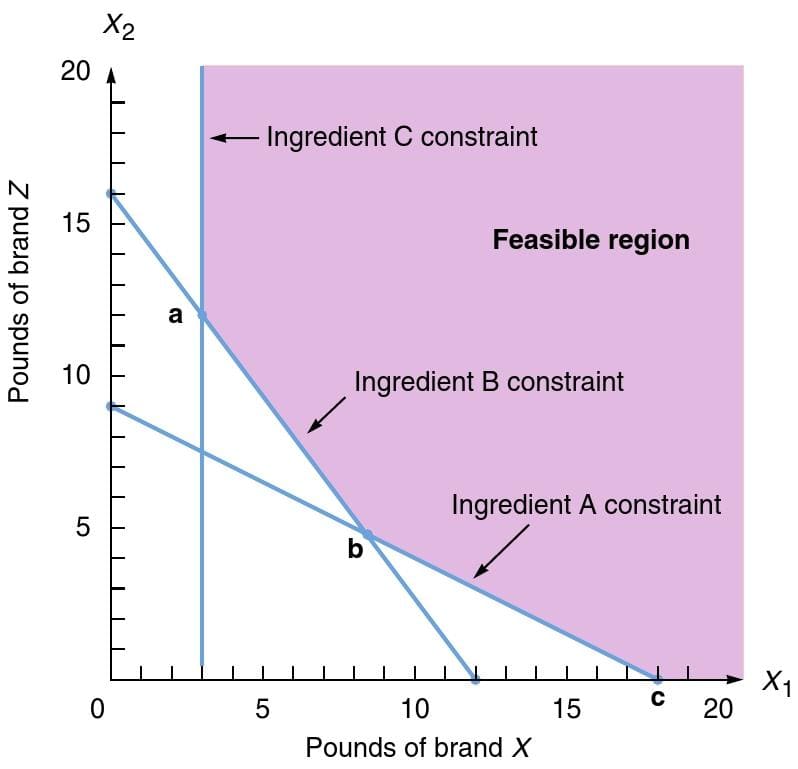
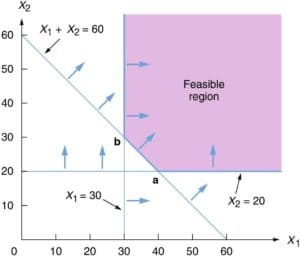
FIGURE A ■ Feasible Region for the Holiday Meal Turkey Ranch Problem

Figure-A illustrates these constraints.

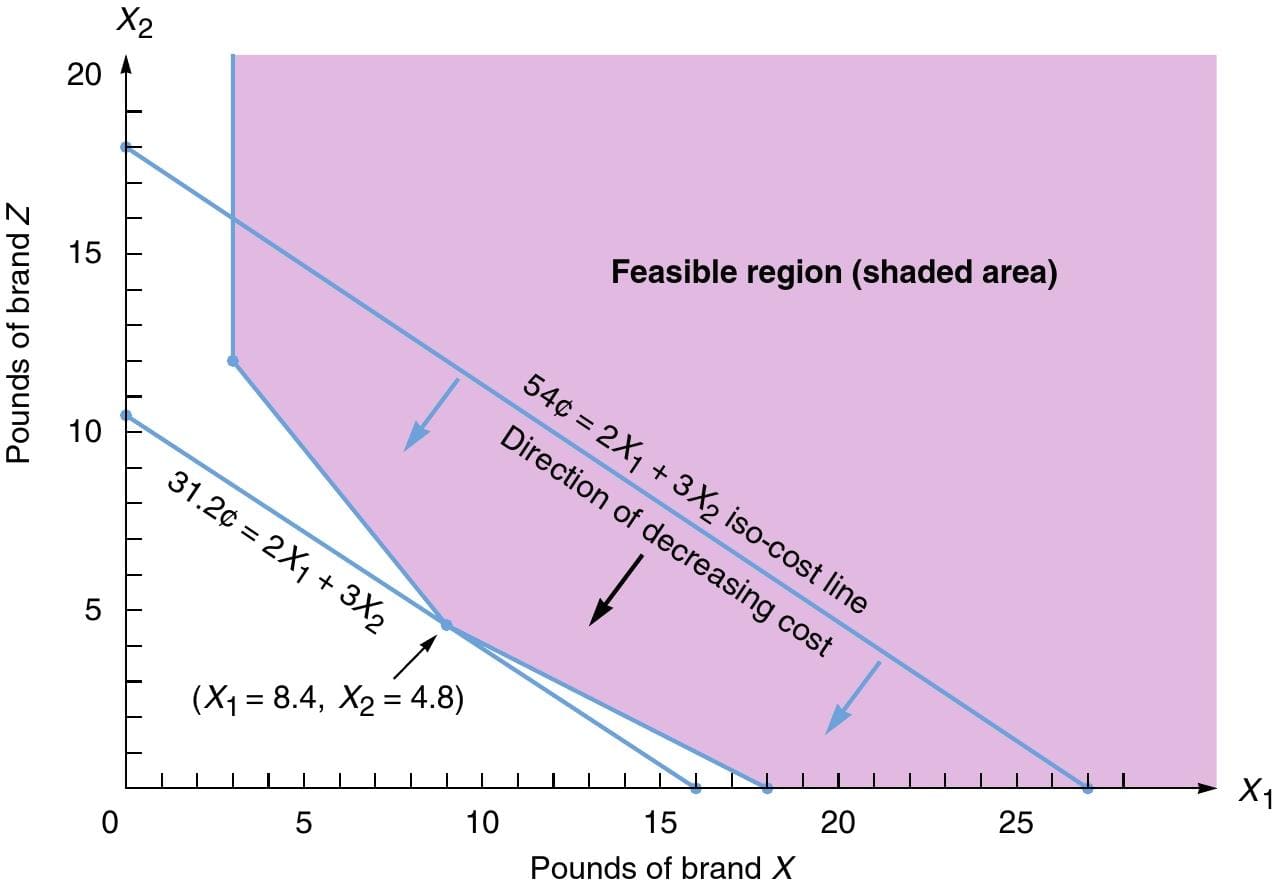
The iso—cost line approach may be used to solve LP minimiza- tion problems such as that of the Holiday Meal Turkey Ranch. As with iso—profit lines, we need not compute the cost at each corner point, but instead draw a series of parallel cost lines. The lowest cost line (that is, the one closest in toward the origin) to touch the feasible region provides us with the optimal solution corner.

For example, We start in Figure B by drawing a 54¢ Cost line, namely, 54=2X₁+3X₂. Obviously, there are many points in the feasible region that would yield a lower total cost. We proceed to move our iso—cost line toward the lower left. in a plane parallel to the 54¢ solution line. The last point we touch while still in contact with the feasible region is the same as corner point b of Figure A. It has the coordinates (X₁=8.4, X₂=4.8) and an associated cost of 31.2 cents.

FIGURE B ■
Graphical Solution to the Holiday Meal Turkey Ranch Problem Using the Iso-Cost Line
Note that the last line parallel to the 54¢ iso-cost line that touches the feasible region indicates the optimal corner point.

💎 Iso-Profit Line Method — Corner-Point Method — Sensitivity Analysis 👈