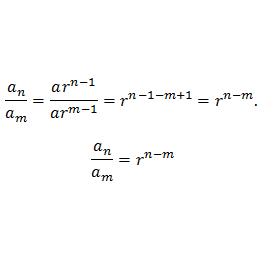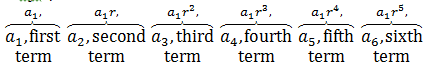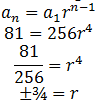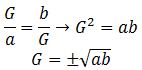How to Find a Certain Term, Given Two Terms in a Geometric Sequence?

The nth Term Of A Geometric Sequence
If {a_n} is a geometric sequence with common ratio r, then

a₂=a₁⋅r
a₃=a₂⋅r=a₁⋅r²
a₄=a₃⋅r=a₁⋅r³
a_n=a₁⋅r^(n-1) for every n>1

Example 1: Finding a Term in a Geometric Sequence
In a geometric sequence, the third term is 24 and the 6th term is 192. Find the 10th term. Solution: Here, a₃=a₁⋅r²=24 … (1)
and a₆=a₁⋅r⁵=192 … (2)
Dividing (2) by (1), we get r=2. Substituting r=2 in (1), we get a=6.
Hence a₁₀=6⋅2⁹=3072.

Example 2. If the first and tenth terms of a geometric sequence are 1 and 4, find the seventeenth term to three decimal places.
Solution:
First let n=10, a₁=1, a₁₀=4 and use the formula a_n=a₁⋅r^(n-1) to find r.

a_n=a₁⋅r^(n-1)
a₁₀=1⋅r^(10-1)
4=r⁹→r=4^(1⁄9)

Now use the formula a_n=a₁⋅r^(n-1) again, this time with n=17.

a₁₇=a₁⋅r¹⁷=1(4^(1⁄9))¹⁷=4^(17⁄9)≈13.716

If we know the first term in a geometric progression and the ratio between successive terms, then we can work out the value of any term in the geometric progression . The nth term is given by

a_n=a₁⋅r^(n-1)
Again, a is the first term and r is the ratio. Remember that a₁⋅r^(n-1)≠(a₁⋅r)^(n-1).

Question 1. Given the first two terms in a geometric progression as 2 and 4, what is the 10th term?
Solution:

a₁=2;r=4/2=2
Then a₁₀=2×2⁹=1024.

Question 2. Given the first two terms in a geometric progression as 5 and ½, what is the 7th term?
Solution:

Example 3. Find the 20th and nth terms of the geometric sequence 5/2, 5/4, ⅝, …
Solution:
The given geometric sequence is 5/2, 5/4, ⅝, … .
Here, a₁= First term =5/2.

Question 3. (Challenge) The fifth term of a geometric sequence is 1/27 of the eighth term. If the ninth term is 702, what is the eighth term?
Solution:
Given a₅=a₈/27 and a₉=702.
Find the Value of r.

Find the Value of a₈.
a₉=a₈⋅r
702=a₈⋅3
a₈=234
Answer: 234

Example 4: Finding Terms in a Geometric Sequence
If the third term of a geometric sequence is -12 and the fourth term is 24, find the first and fifth terms of the sequence.
Solution:
Divide the 4th term by the 3rd term to find the common ratio.
The common ratio is 24/(-12) or -2. Substitute 3 for n and -2 for r to find the first term.

a_n=a₁⋅r^(n-1)
a₃=a₁⋅(-2)^(3-1)
-12=a₁⋅(-2)²
-12=4a₁
-3=a₁
The first term is -3. Find the fifth term.
a_n=a₁⋅r^(n-1)
a₅=-3(-2)^(5-1)
=-3(-2)⁴
a₅=-48
The fifth term is -48.

Example 5: Determining Terms and the Number of Terms in a Finite Geometric Sequence
In a finite geometric sequence, t₁=5 and t₅=1280
a) Determine t₂ and t₆.
b) The last term of the sequence is 20, 480. How many terms are in the sequence?
solution:
a) Determine the common ratio.
Use: t_n=t₁ r^(n-1)
Substitute: n=5, t₅=1280, t₁=5

1280=5r^(5-1)
Simplify.
1280=5r⁴
Divide each side by 5.
256=r⁴
Take the fourth root of each side.
16=r²
r=-4 or r=4
There are 2 possible values for r.
(i) When r=-4, then t₂ is 5(4)=20
(ii) When r=4, then t₂ is 5(-4)=-20
To determine t₆, use: t_n=t₁ r^(n-1)
(i) Substitute: n=6, t₁=5, r=-4
t₆=5(-4)^(6-1)=5(-4)⁵=-5120
(ii) Substitute: n=6, t₁=5, r=4
t₆=5⋅4^(6-1)=5⋅4⁵=5120
So, t₂ is -20 or 20, and t₆ is -5120 or 5120.

b) Since the last term is positive, use the positive value of r.

t_n=t₁ r^(n-1)
Substitute: t_n=20 480, t₁=5, r=4
20480=5⋅4^(n-1)
Divide each side by 5.
4096=4^(n-1)
Use guess and test to determine which power of 4 is equal to 4096.
Guess: 4⁴=256
This is too low. Guess: 4⁶=4096
This is correct.
So, 4⁶=4^(n-1)
Equate exponents.
6=n-1
n=7
There are 7 terms in the sequence.

Ratio of two terms of Geometric Sequence
Let the geometric sequence be

a, ar, a₁⋅r², …
Now,

Example 6. The 5th, 8th and 11th terms of a geometric sequence are p, q and s, respectively. Show that q²=p⋅s.
Solution:
Let a be the first term and r be the common ratio of the geometric sequence
According to the given condition,