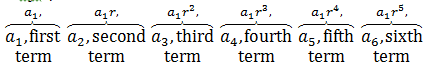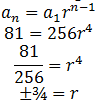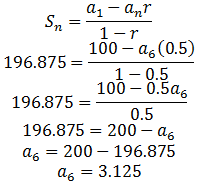How to Find a Certain Term in a Geometric Sequence?

The formula for the nth term involves four variables: a_n, a₁, r, and n. If we know the value of any three of them, we can find the value of the fourth.

Explicit geometric sequences also have a formula for finding any term in a sequence.

a_n=a₁ r^(n-1)
a_n= the term in the sequence you are trying to find (n represents the desired term number)
a₁= the first term in the sequence
r= the common ratio

Example 1. What is the 15th term of the geometric sequence -9, 27, -81, … ?
Solution:
Calculate the common ratio.

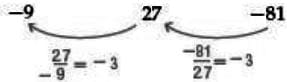
The common ratio is -3.
a_n=a₁ r^(n-1)
a₁₅=-9⋅(-3)^(15-1)
=-9⋅(-3)¹⁴
=-43,046,721
The 15th term of the sequence is -43,046,721.

Ex2. What is the 10th term of the geometric sequence 6, -24, 96, … ?
Solution:
Calculate the common ratio.

The common ratio is -4.
a_n=a₁ r^(n-1)
a₁₀=6⋅(-4)^(10-1)
=6⋅(-4)⁹
=-1,572,864
The 10th term of the sequence is -1,572,864.

Ex3. Find the eleventh term of the sequence 3, -6, 12, -24, …
(A). 1024 (B). 3072 (C). 33 (D). -6144
Solution:
Calculate the common ratio.

The common ratio is -2.
a_n=a₁ r^(n-1)
a₁₁=3(-2)^(11-1)
=3(-2)¹⁰
a₁₁=3072
The eleventh term of the sequence is 3072. Choice B is the correct answer.

Ex4 — Ex10: Find the specified term for each geometric sequence or sequence with the given characteristics
Ex4. a₉ for 60, 30, 15, … .
Solution:
First, find the common ratio.

30÷60=½
15÷30=½
Use the formula for the nth term of a geometric sequence to find a₉.

Ex5. a₄ for 7, 14, 28, … .
Solution:
First, find the common ratio.

14÷7=2
28÷14=2
Use the formula for the nth term of a geometric sequence to find a₄.
a_n=a₁ r^(n-1)
a₄=7⋅2^(4-1)
a₄=7⋅8
a₄=56

Ex6. a₅ for 3, 1, ⅓, … .
Solution:
First, find the common ratio.

1÷3=⅓
⅓÷1=⅓
Use the formula for the nth term of a geometric sequence to find a₅.

Ex7. a₆ for 540, 90, 15, … .
Solution:
First, find the common ratio.

90÷540=⅙
15÷90=⅙
Use the formula for the nth term of a geometric sequence to find a₆.

Ex8. a₇ if a₃=24 and r=0.5.
Solution:

a₇=a₃ r^(7-3)
a₇=24⋅½⁴
a₇=1.5

Ex9. a₆ if a₃=32 and r=-0.5.
Solution:

a₆=a₃ r^(6-3)
a₆=32⋅(-½)³
a₆=32⋅(-⅛)
a₆=-4

Ex10. a₈ if a₁=4096 and r=¼.
Solution:
Use the formula for the nth term of a geometric sequence to find a₈.

Ex11 — Ex14: Find the indicated term of the geometric sequence

Ex11. The 10th term; 6, 18, 54, 162, …
Solution:
First develop a formula for a_n; first term is 6 and common ratio is 3.

a_n=x(3ⁿ)
a₁=x(3¹)
6=3x
2=x
Now, find the 10th term: a₁₀=2(3¹⁰)=118098
Answer: 118098

Ex12. The 9th term; 5, 20, 80, 160, …
Solution:
First develop a formula for a_n; first term is 5 and common ratio is 4

formula for a_n=5/4 (4ⁿ).
Now, find the 9th term: a₉=5/4 (4⁹)=327680
Answer: 327680

Ex13. The 14th term; 200, 100, 50, 25, …
Solution:
First develop a formula for a_n; first term 200, common ratio ½.

a_n=x(½ⁿ)
a₁=x(½¹)
200=½x
2⋅200=2⋅½x
x=400
formula for a_n=400(½ⁿ).
Now, find the 14th term: a₁₄=400(½¹⁴)=25/1024
Answer: 25/1024

Ex14. The 20th term; 39366, 13122, 4374, …
Solution:
First develop a formula for a_n; first term 39366 common ratio ⅓.

a_n=x(⅓ⁿ)
a₁=x(⅓¹)
39366=⅓x
3⋅39366=3⋅⅓x
x=118098
a_n=118098(⅓ⁿ)
now I can find a₂₀=118098(⅓²⁰)=2/59049
Answer: 2/59049

Ex15. Find 4th term in the geometric sequence 5, 10, 20, …
Solution:

a=5, r=10/5=2, a_n=?
a_n=ar^(n-1)
a₄=5⋅2^(4-1)=5×8=40

Ex16. Determine the 10th term of the sequence: 3, 6, 12, …
Solution:

a=3, r=6/3=12/6=2
a_n=ar^(n-1)
a₁₀=3⋅2^(10-1)=3⋅2⁹=3⋅512=1536

Ex17. Find the 7th term in the following sequence: 6, 18, 54, 162, …
Solution:
Finding the common ratio can be harder than finding the common difference. One way to find it is the divide each term by the term before it.
18÷6=3, 54÷18=3, 162÷54=3. So the common ratio is 3.

a₇=6⋅3^((7-1)))
a₇=6⋅3⁶=6×729
a₇=4,374
So the 7th term of the sequence is 4,374.

Ex18. Find the 8th term in the following sequence: 96, 48, 24, 12, 6, …
Solution:
To find the common ratio, divide each term by the one before it.
48÷96=½, 24÷48=½, 12÷24=½. The common ratio is ½.

The 8th term of the sequence is 0.75.

Ex19. What is the 10th term of the sequence 4, 12, 36, 108, 324, … ?
Solution:
The sequence 4, 12, 36, 108, 324, … is a geometric sequence with a₁=4 and r=3.Therefore,

a_n=a₁ r^(n-1)
a₁₀=4⋅3⁹=78732
Use a calculator for the computation.

Ex20: Find the Next Term

Test-Taking Tip
Since the terms of this sequence are increasing, the missing term must be greater than 125. You can immediately eliminate 75 as a possible answer.

Multiple-Choice Test Item
Find the missing term in the geometric sequence: 8, 20, 50, 125, _
(A). 75 (B). 200 (C). 250 (D). 312.5
Solution:
Since 20/8=2.5, 50/20=2.5, and 125/50=2.5, the sequence has a common ratio of 2.5.
Solve the Test Item
To find the missing term, multiply the last given term by 2.5:

125(2.5)=312.5.
The answer is D.

Ex21. The first term of a geometric series is 1 and the common ratio is 9. What is the 8th term of the sequence?
Solution:

a_n=a₁ r^(n-1)
a₈=1⋅9^(8-1)
=1⋅9⁷
=4,782,969
The 8th term of the sequence is 4,782,969.

Ex22. The first term of a geometric series is 2 and the common ratio is 4. What is the 14th term of the sequence?
Solution:

a_n=a₁ r^(n-1)
a₁₄=2⋅4^(14-1)
=2⋅4¹³
=134, 217, 728
The 14th term of the sequence is 134, 217, 728.

Ex23: Finding a missing term
Find the first term of a geometric sequence whose fourth term is 8 and whose common ratio is ½.
Solution:
Let a₄=8, r=½, andn n=4 in the formula a_n=a₁ r^(n-1).

8=a₁⋅½^(4-1)
8=a₁⋅⅛
64=a₁
So the first term is 64.

Ex24. If r=4 and a₈=100, what is the first term of the geometric sequence?
Solution:
Substitute a₈=100, r=4, and n=8 into the formula for the nth term of a geometric sequence to find the a₁.

Ex25: Find a Term Given the Fourth Term and the Ratio
Find the tenth term of a geometric sequence for which a₄=108 and r=3.
Solution:
First, find the value of a₁. Formula for nth term, a_n=a₁⋅r^(n-1).

n=4, r=3
a₄=a₁⋅3^(4-1)
a₄=108
108=27a₁
Divide each side by 27. Formula for nth term, a_n=a₁⋅r^(n-1).
n=10, a₁=4, r=3
a_n=a₁⋅r^(n-1)
a₁₀=4⋅3^(10-1)
a₁₀=78, 732

Ex26. Determine the 12th term of a geometric sequence whose 8th term is 192 and the common ratio is 2.
Solution: We have

Ex27. Find the eighth term of a geometric sequence for which a₃=81 and r=3.
Solution:
Because a₃=81, the third term in the sequence is 81. To find the eighth term of the sequence, you need to find the 1st term of the sequence. Use the nth term of a Geometric Sequence formula.

a_n=a₁ r^(n-1)
a₃=a₁⋅3^(3-1)
81=a₁⋅9
a₁=9
Then the first term a₁ is 9.
Use a₁ to find the eighth term of the sequence.
a_n=a₁ r^(n-1)
a₈=a₁⋅3^(8-1)
=9⋅3⁷
=19,683
The eighth term of the geometric sequence is 19,683.

Ex28. Find the 12th term of a geometric sequence whose 8th term is 192 and the common ratio is 2.
Solution:
Common ratio, r=2
Let a be the first term of the geometric sequence.

Ex29: Find a Particular Term
Find the eighth term of a geometric sequence for which a₁=-3 and r=-2.
Solution:
Formula for nth term, a_n=a₁⋅r^(n-1).

n=8, a₁=-3, r=-2
a₈=(-3)⋅(-2)^(8-1)
a₈=(-3)⋅(-128)
a₈=384
The eighth term is 384.

Ex30. Find the sixth term of a geometric sequence with a first term of 9 and a common ratio of 2.
Solution:
Use the formula for the nth term of a geometric sequence to find the a₆.

a_n=a₁ r^(n-1)
a₆=9⋅2^(6-1)
a₆=288

Ex31: Using the Formula for the General Term of a Geometric sequence
Find the eighth term of the geometric sequence whose first term is -4 and whose common ratio is -2.
Solution:
To find the eighth term, a₈, we replace n in the formula with 8, a₁ with -4, and r with

a_n=a₁ r^(n-1)
a₈=-4(-2)^(8-1)=-4(-2)⁷=-4(-128)=512
The eighth term is 512. We can check this result by writing the first eight terms of the Growth sequence:
-4, 8, -16, 32, -64, 128, -256, 512.

Ex32. (Biology) A certain bacteria grows at a rate of 3 cells every 2 minutes. If there were 260 cells initially, how many are there after 21 minutes?
Solution:
Given, a₁=260, n=21 and r=3/2

Answer: 864,567

Ex33. (Biology) A virus goes through a computer, infecting the files. If one file was infected initially and the total number of files infected doubles every minute, how many files will be infected in 20 minutes?
Solution:
Given, a₁=1, r=200% or 2, n=20.

a_n=a₁ r^(n-1)
a₂₀=1⋅2^(20-1)
=524,288
Answer: 524,288

Ex34. (Short Response) Elisa has a savings account. She withdraws half of the contents every year. After 4 years, she has $2000 left. How much did she have in the savings account originally?
Solution:
Given n=4, a₄=2000, r=0.5

She have invested (a⁰) $32, 000.
Answer: $32, 000

Ex35. (Sense-Making)
A certain drug has a half-life of 8 hours after it is administered to a patient. What percent of the drug is still in the patient’s system after 24 hours?
Solution:
Given a₁=100% or 1 and r=½ and n=4.