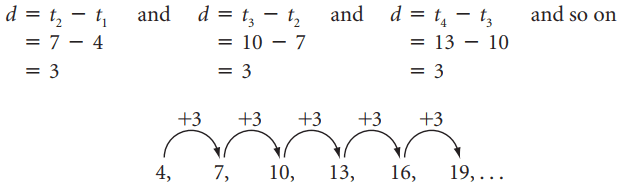How to Find a Term from the Last Term of an Arithmetic Progression?

Arithmetic progressions
Consider these two common sequences
1, 3, 5, 7, …,
and
0, 10, 20, 30, 40, …, .
It is easy to see how these sequences are formed. They each start with a particular first term, and then to get successive terms we just add a fixed value to the previous term. In the first sequence we add 2 to get the next term, and in the second sequence we add 10. So the difference between consecutive terms in each sequence is a constant. We could also subtract a constant instead, because that is just the same as adding a negative constant. For example, in the sequence
8, 5, 2, -1, -4, …,
the difference between consecutive terms is -3. Any sequence with this property is called an arithmetic progression, or AP for short.

We can use algebraic notation to represent an arithmetic progression. We shall let a stand for the first term of the sequence, and let d stand for the common difference between successive terms. For example, our first sequence could be written as

1,	3,	5,	7,	9,	…,
1,	1+2,	1+2×2,	1+3×2,	1+4×2,	…,

and this can be written as

a, a+d, a+2d, a+3d, a+4d, …
where a=1 is the first term, and d=2 is the common difference. If we wanted to write down the n-th term, we would have
a+(n-1)d,
because if there are n terms in the sequence there must be (n-1) common differences between successive terms, so that we must add on (n-1)d to the starting value a. We also sometimes write ℓ for the last term of a finite sequence, and so in this case we would have
ℓ=a+(n-1)d.

Key Point
An arithmetic progression, or AP, is a sequence where each new term after the first is obtained by adding a constant d, called the common difference, to the preceding term. If the first term of the sequence is a then the arithmetic progression is

a, a+d, a+2d, a+3d, …
where the n-th term is a+(n-1)d.

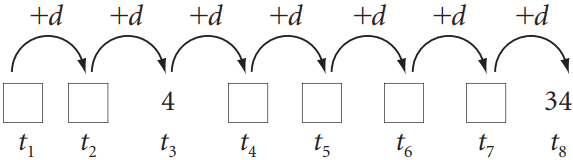
Question 1. Find the 11th term from the last term (towards the first term) of the AP: 10, 7, 4, …, -62.
Solution:
Here, a=10, d=7-10=-3, ℓ=-62,
where ℓ=a+(n-1)d
To find the 11th term from the last term, we will find the total number of terms in the AP.

-62=10+(n-1)(-3)
-72=(n-1)(-3)
n-1=24
n=25
So, there are 25 terms in the given AP.
The 11th term from the last term will be the 15th term. (Note that it will not be the 14th term. Why?)
So, a₁₅=10+(15-1)(-3)=10-42=-32
i.e., the 11th term from the last term is -32.
Alternative Solution:
If we write the given AP in the reverse order, then a=-62 and d=3 (Why?)
So, the question now becomes finding the 11th term with these a and d.
So, a₁₁=-62+(11-1)×3=-62+30=-32
So, the 11th term, which is now the required term, is -32.

Question 2. Find the 20th term from the last term of the AP: 3, 8, 13 …, 253.
Solution:
The 20th term from the last term of the AP: 3, 8, 13 …, 253 = the 20th term from the beginning of the AP:

253, …, 13, 8, 3.
In the A.P.: 253, …, 13, 8, 3, first term =253 and common difference =3-8=-5.
Therefore, a₂₀=a+19d
⇒a₂₀=253+19(-5)=253-95=158
Let’s read post Sum Formula for every Arithmetic Series with Given the First and Last Terms.
Ex3. Find the 8th term from the end of the arithmetic sequence 7, 10, 13, …, 184.
Solution:
Here, a=7 and d=(10-7)=3, ℓ=184 and n=8th form the end.
Now, nth term from the end =[ℓ-(n-1)d].
8th term from the end =[184-(8-1)⋅3]
=[184-(7⋅3)]=(184-21)=163
Hence, the 8th term from the end is 163.

Ex4. Find the 6th term form the end of the arithmetic sequence 17,14,11,…,(-40).
Solution:
Here, a=7 and d=(14-17)=-3, ℓ=(-40) and n=6.
Now, nth term from the end =[ℓ-(n-1)d].
6th term from the end =[(-40)-(6-1)⋅(-3)]