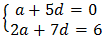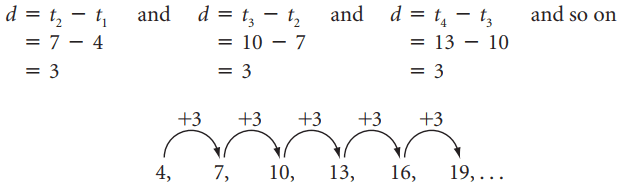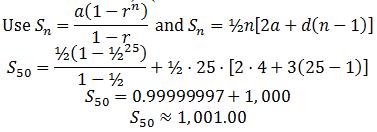Example 1: Find a Particular Term
Construction.
The table below shows typical costs for a construction company to rent a crane for one, two, three, or four months.

Months	Cost ($)
1	75,000
2	90,000
3	105,000
4	120,000

Refer to the information above. Assuming that the arithmetic sequence continues, how much would it cost to rent the crane for twelve months?
Explore
Since the difference between any two successive costs is $15,000, the costs form an arithmetic sequence with common difference 15,000.
Plan
You can use the formula for the nth term of an arithmetic sequence with a₁=75,000 and d=15,000 to find a₁₂, the cost for twelve months.
Solve
Formula for nth term, a_n=a₁+(n-1)d.

n=12, a, =75,000, d=15,000
a₁₂=75,000+(12- 1)15,000
a₁₂=240,000
It would cost $240,000 to rent the crane for twelve months.
Examine
You can find terms of the sequence by adding 15,000. a₅ through a₁₂ are 135,000, 150,000, 165,000, 180,000, 195,000, 210,000, 225,000, and 240,000. Therefore, $240,000 is correct.

Example 2
Scott is saving to buy a guitar. In the first week, he put aside $42 that he received for his birthday, and in each of the following weeks, he added $8 to his savings. He needs $400 for the guitar that he wants. In which week will he have enough money for the guitar?
solution:
Let a₁=42 and d=8.
The value for n for which a_n=400 is the week Scott will have enough money to buy the guitar.

a_n=a₁+(n-1)d
400=42-(n-1)(8)
400=42-8n-8
400=34-8n
366=8n
45.75=n
Scott adds money to his savings in $8 increments, so he will not have the needed $400 in savings until the 46th week.
answer: 46th week

Example 3: Find the indicated term in each arithmetic sequence.
a). 50th term of, 3, 6, 9, 12, …

First I need a formula for a_n;

a_n=3n+x
a₁=3(1)+x
3=3+x
0=x
Formula for sequence: a_n=3n.
Computation of 50th term: a₅₀=3(50)=150
Answer: 150

b). 100th term of 5, 8, 11, 14, …

First I need a formula for a_n:

a_n=3n+x
a₁=3(1)+x
5=3+x
2=x
Formula for sequence: a_n=3n+2.
Computation of 100th term: a₁₀₀=3(100)+2=302 Answer: 302

c). 80th term of 5, 2, -1, -4, …

First I need a formula for a_n:

a_n=-3n+x
a₁=-3(1)+x
5=-3+x
8=x
Formula for sequence: a_n=-3n+8.
Computation of 80th term: a₈₀=-3(80)+8=-232
Answer: -232

d). 25th term of 20, 18, 16, 14, …

First I need a formula for a_n:

a_n=-2n+x
a1=-2(1)+x
20=-2+x
22=x
Formula for sequence: a_n=-2n+22.
Computation of 25th term: a₂₅=-2(25)+22
Answer: -28

e). A local theater has 30 seats in the first row and 50 rows in all. Each successive row contains two additional seats. How many seats are in the 50th row of the theater?
solution:
This is just an arithmetic sequence problem with a₁=30, and d=2. I need to find a₅₀. First I will get a formula for a_n.

a_n=2n+x
a₁=2(1)+x
30=2+x
28=x
Formula for sequence: a_n=2n+28.
Now, to find the number of seats in the 50th row: a₅₀=2(50)+28=128
Answer: There are 128 seats in the 50th row.

f). An outdoor amphitheater has 40 seats in the first row, 41 seats in the second row, 42 seats in the third row. The pattern continues. The amphitheater has 40 rows. How many seats are in the 30th row of the theater?

solution:
This is just an arithmetic sequence problem with a₁=40, and d=1. I need to find a₄₀. First I will get a formula for a_n.
a_n=1n+x
a₁=1(1)+x
40=1+x
39=x
Formula for sequence: a_n=n+39.
Now, to find the number of seats in the 40th row: a₄₀=40+39=79
Answer: There are 79 seats in the 40th row.

4. What is the 10th term of the following sequence?

1, 5, 9, 13, …
a₁₀=1+(10-1)4
a₁₀=1+9⋅4=1+36
a₁₀=37
So the 10th term of this sequence is 37.

5. What is the 12th term of the following sequence?

34, 31, 28, 25, 22, …
a₁₂=34+(12-1)(-3)
a₁₂=34+11(-3)=34-33
a₁₂=1
The 12th term of this sequence is 1.

6. Find the 7th term of A.P. in which the first term is 7 and the common difference is -3.
Solution:

a₇=7th term=?
a₁=7; d=3
Putting these values in a_n=a+(n-1)d
a₇=7+(7-1)(-3)
=7+6(-3)
=7-18
a₇=-11

7. Find the 9th term of the A.P. -5/4, -¼, ¾, …
Solution:

a₁=a=-5/4=-1¼;a₂=-¼;a₃=¾;
d=a₂–a₁=a₃–a₂=?
d=-¼-(-1¼)=¾-(-¼)=4/4
d=1

9th term =a₉=?

a_n=a+(n-1)d
a₉=-1¼+(9-1)1
a₉=-1¼+8=8-1-¼
a₉=6¾

8. For the arithmetic sequence 100, 97, 94, 91, … , find:
a. the common difference.
b. the 20th term of the sequence.
solution:
a. The common difference is the difference between any term and the previous term:

97-100=-3 or 94-97=-3 or 91-95=-3
The common difference is -3.
b. a₂₀=100-(20-1)(-3)
=100-(19)(-3)
=100-57=43
The 20th term can also be found by writing the sequence:
100, 97, 94, 91, 88, 85, 82, 79, 76, 73, 70, 67, 64, 61, 58, 55, 52, 49, 46, 43
answer:
a. d=-3 b. a₂₀=43

9. If the first 3 terms in an arithmetic progression are 3, 7, 11 then what is the 10th term? The first term is a=3, and the common difference is d=4.

u_n=a+(n-1)d
u₁0=3+(10-1)4
=3+9×4=39

10. If the first 3 terms in an arithmetic progression are 8, 5, 2 then What is the 16th term? In this progression a=8 and d=-3.

u_n=a+(n-1)d
u₁₆=8+(16-1)(-3)
=-37

11. Find the 10th term of the AP: 2, 7, 12, …
Solution: Here, a=2, d=7-2+5 and n=10. We have a_n=a+(n-1)d.
So, a₁₀+(10-1)×5=2+45=47
Therefore, the 10th term of the given AP is 47.

⇒a_n=3.5+0=3.5

12. Choose the correct choice in the following and justify:
(i) 30th term of the A.P.: 10, 7, 4, …, is
(A) 97 (B) 77 (C) -77 (D) -87
(ii) 11th term of the A.P.: -3, -½, 2, …, is
(A) 28 (B) 22 (C) -38 (D) -48½
Solutions:
(i) Here, a=10, d=7-10=-3 and n=30. Therefore, putting the values in a_n=a+(n-1)d, we get

a₃₀=10+(30-1)(-3)
⇒a₃₀=10-87=-77
Hence, the option (C) is correct.

(ii) Here, a=-3, d=-½-(-3)=2½ and n=11. Therefore, putting the values in a_n=a+(n-1)d, we get

a₁₁=-3+(11-1)(2½)
⇒a₁₁=-3+25=22
Hence, the option (B) is correct.