We have defined the arithmetic mean of two numbers as their average, that is, the sum of the numbers divided by 2. For example, the arithmetic mean of 4 and 28 is (4+28)/2=32/2=16. The numbers 4, 16, and 28 form an arithmetic sequence with a common difference of 12.
We can find three numbers between 4 and 28 that together with 4 and 28 form an arithmetic sequence: 4, a₂, a₃, a₄, 28. This is a sequence of five terms.
1. Use the formula for a₅ to find the common difference:

a₅=a₁+(n-1)d
28=4+(5-1)d
28=4+4d
24=4d
6=d
2. Now use the recursive formula, a_n=a_(n-1)+d, and d=6, to write the sequence:
4, 10, 16, 22, 28.
The numbers 10, 16, and 22 are three arithmetic means between 4 and 28. Looking at it another way, in any arithmetic sequence, any given term is the average of the term before it and the term after it. Thus, an arithmetic mean is any term of an arithmetic sequence.

Arithmetic Means

Sometimes you are given two terms of a sequence, but they are not successive terms of that sequence. The terms between any two non-successive terms of an arithmetic sequence are called arithmetic means. In the sequence below, 41, 52, and 63 are the three arithmetic means between 30 and 74.

3 arithmetic means between 30 and 74

Example 1: Find Arithmetic Means
Find the four arithmetic means between 16 and 91.

You can use the nth term formula to find the common difference. In the sequence 16, ? , ? , ? , ? , 91, …, a₁ is 16 and a₆ is 91.
Formula for the nth term, a_n=a₁+(n-1)d.

a₆=a₁+(6-1)d
a₁=16, a₆=91, n=6
91=16+5d
⅕(91-16)=d
d=15
Now use the value of d to find the four arithmetic means.

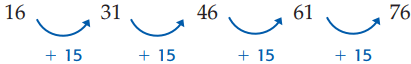
The arithmetic means are 31, 46, 61, and 76. CHECK 76+15=91 ✓

Study Tip
Alternate Method
You may prefer this method. The four means will be 16+d, 16+2d, 16+3d, and 16+4d. The common difference is d=91-(16+4d) or d=15.

Example 2. Insert four numbers between 3 and 12 so that all six numbers are in arithmetic sequence.
solution:
Suppose the common difference is d.
∴ the numbers are 3, 3+d, 3+2d, 3+3d, 3+4d, and 12

3+5d=12
5d=9→d=9/5=1.8
So, the sequence is 3, 4.8, 6.6, 8.4, 10.2, 12.

Example 3. Find five arithmetic means between 2 and 23.
solution:
Five arithmetic means between 2 and 23 will form a sequence of seven terms. Use the formula for a₇ to find the common difference:

a₇=a₁+(n-1)d
23=2-(7-1)d
23=2-6d
21=6d
7/2=d
Evaluate a₂, a₃, a₄, a₅, and a₆:

Answer: The five arithmetic means are 5½, 9, 12½, 16, and 19½.

Arithmetic Means between a and b

The number A₁, A₂, A₃, …, A_n are said to be n arithmetic means between a and b if a, A₁, A₂, A₃, …, A_n, b are in A.P. We may obtain the arithmetic means between two numbers by using a_n=a+(n-1)d to find d, and the means can then be computed.

Example 4. Insert three A.M’s between-18 and 4.
Solution:
Let A₁, A₂, A₃ be the required A.M’s between-18 and 4, then-18, A₁, A₂, A₃, 4 are in A.P.
Here a=-18, n=5, a₅=4, d=? Using a_n=a+(n-1)d
a₅=-18+(5-1)d
4=-18+4d
4+18=4d
d=22÷4=5½
Therefore A₁=2nd term=a+d
=-18+5½=-12½
A₂=3rd term=A₁+d=-12½+5½=-7
Thus the required A.M’s are-12, -7, -1½.

Series:

The sum of the terms of a sequence is called as ‘series’. For example: 1, 4, 9, 16, … is a sequence. Sum of the terms of sequence i.e., 1+4+9+16+… represent a series.

Example 5. Insert five numbers between 8 and 26 such that the resulting sequence is an A.P.
Solution:
Let A₁, A₂, A₃, A₄, and A₅ be five numbers between 8 and 26 such that 8, A₁, A₂, A₃, A₄, A₅, 26 is an A.P.
Here, a=8, b=26, n=7
Therefore, 26=8+(7-1)d

6d=26-8=18
d=3
A₁=a+d=8+3=11
A₂=a+2d=8+2⋅3=8+6=14
A₃=a+3d=8+3⋅3=8+9=17
A₄=a+4d=8+4⋅3=8+12=20
A₅=a+5d=8+5⋅3=8+15=23
Thus, the required five numbers between 8 and 26 are 11, 14, 17, 20, and 23.

Example 6. Suppose {a_n} is an arithmetic sequence with a₈=6 and a₁₂=-4. Find a, d, and the three terms between a₈ and a₁₂.
Solution:
From Equation (1), a₈=a+7d, and a₁₂=a+11d, from which the difference is given by a₁₂–a₈=4d. Use the given values for :18 and an to get-4-6=4d, or d=-5/2 Substitute-5/2 for din 6=a+7d and solve for a, a=47/2. Find the three terms between a₈ and a₁₂ by successively adding-5/2:

a₉=a₈-5/2=7/2, a₁₀=a₉-5/2=1, a₁₁=a₁₀-5/2=-3/2.
Therefore, a₉ is 7/2, a₁₀ is 1, and a₁₁ is-3/2.

Arithmetic mean

Given two numbers a and b. We can insert a number A between them so that a, A, b is an A.P. Such a number A is called the arithmetic mean (A.M.) of the numbers a and b. Note that, in this case, we have

A-a=b-A→A=½(a+b)

We may also interpret the A.M. between two numbers a and b as their a+b average ½(a+b). For example, the A.M. of two numbers 4 and 16 is 10. We have, thus constructed an A.P. 4, 10, 16 by inserting a number 10 between 4 and 16. The natural question now arises: Can we insert two or more numbers between given two numbers so that the resulting sequence comes out to be an A.P.? Observe that two numbers 8 and 12 can be inserted between 4 and 16 so that the resulting sequence 4, 8, 12, 16 becomes an A.P.

More generally, given any two numbers a and b, we can insert as many numbers as we like between them such that the resulting sequence is an A.P.

Let A₁, A₂, A₃, …, A_n be n numbers between a and b such that a, A₁, A₂, A₃, …, A_n, b is an A.P.
Here, b is the (n+2)th term, i.e., b=a+[(n+2)-1]d=a+(n+1)d.
This gives

Thus, n numbers between a and b are as follows:

(The general Arithmetic Mean formula)
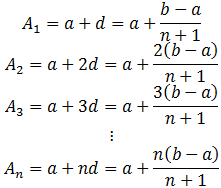
Example 7. Insert 6 numbers between 3 and 24 such that the resulting sequence is an A.P.
Solution: Let A₁, A₂, A₃, A₄ A₅ and A₆ be six numbers between 3 and 24 such that 3, A₁, A₂, A₃, A₄ A₅, A₆, 24 are in A.P. Here, a=3, b=24, n=8. Therefore, 24=3+(8-1)d, so that d=3.
Thus A₁=a+d=3+3=6; A₂=a+2d=3+2×3=9;
A₃=a+3d=3+3×3=12; A₄=a+4d=3+4×3=15;
A₅=a+5d=3+5×3=18; A₆=a+6d=3+6×3=21.
Hence, six numbers between 3 and 24 are 6, 9, 12, 15, 18 and 21.