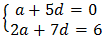Question 1: Writing an Arithmetic Sequence
Write the first 5 terms of:
a) an increasing arithmetic sequence
b) a decreasing arithmetic sequence
Solution:
a) Choose any number as the first term; for example, t₁=-7.
The sequence is to increase, so choose a positive common difference; for example, d=2. Keep adding the common difference until there are 5 terms.

The arithmetic sequence is:-7,-5,-3,-1, 1, …
b) Choose the first term; for example, t₁=5.
The sequence is to decrease, so choose a negative common difference; for example, d=-3.

The arithmetic sequence is: 5, 2,-1,-4,-7, …

Question 2: show that each sequence is arithmetic. Find the common difference and write out the first 4 terms.
a) a_n=3n+5

a₁=3(1)+5=8
a₂=3(2)+5=11
a₃=3(3)+5=14
a₄=3(4)+5=17
Answer:
common difference=3 first 4 terms; 8, 11, 14, 17
b) a_n=5n-2

a₁=5(1)-2=3
a₂=5(2)-2=8
a₃=5(3)-2=13
a₄=5(4)-2=18
Answer:
common difference=5 first 4 terms; 3, 8, 13, 18
c) a_n=3-4n

a₁=3-4(1)=-1
a₂=3-4(2)=-5
a₃=3-4(3)=-9
a₄=3-4(4)=-16
Answer:
common difference=-4 first 4 terms;-1,-5,-9,-16
d) a_n=4-6n

a₁=4-6(1)=-2
a₂=4-6(2)=-8
a₃=4-6(3)=-14
a₄=4-6(4)=-20
Answer:
common difference=-6 first 4 terms;-2,-8,-14,-20

Question 3. Write first four terms of the AP, when the first term a and the common difference d are given as follows:
(i) a=10, d=10 (ii) a=-2, d=0
(iii) a=4, d=-3 (iv) a=-1, d=½
(v) a=-1.25, d=-0.25
Solution:
(i) a=10, d=10
First term a₁=a=10
Second term a₂=a₁+d=10+10=20
Third term a₃=a₂+d=20+10=30
Fourth term a₄=a₃+d=30+10=40

(ii) a=-2, d=0
First term a₁=a=-2
Second term a₂=a₁+d=-2+0=-2
Third term a₃=a₂+d=-2+0=-2
Fourth term a₄=a₃+d=-2+0=-2

(iii) a=4, d=-3
First term a₁=a=4
Second term a₂=a₁+d=4-3=1
Third term a₃=a₂+d=1-3=-2
Fourth term a₄=a₃+d=-2-3=-5

(iv) a=-1, d=½
First term a₁=a=-1
Second term a₂=a₁+d=-1+½=-½
Third term a₃=a₂+d=-½+½=0
Fourth term a₄=a₃+d=0+½=½

(v) a=-1.25, d=-0.25
First term a₁=a=-1.25
Second term a₂=a₁+d=-1.25-0.25=-1.50
Third term a₃=a₂+d=-1.50-0.25=-1.75
Fourth term a₄=a₃+d=-1.75-0.25=-2.00

Question 4. In the following APs, find the missing terms in the boxes:
(i) 2, _, 26
(ii) _, 13, _, 31
(iii) 5, _, _, 9½
(iv)-4, _, _, _, _, 6
(v) _, 38, _, _, _, 22
Solution:
(i) Here, a=2 and a₃=26 to find a₂.
Given that: a₃=a+(3-1)d=26

⇒2+2d=26
⇒d=12
Therefore, a₂=a+(2-1)d=2+12=14

(ii) Here, a₂=13 and a₄=3 to find a₁ and a₃.
Given that: a₂=a+(2-1)d=13

⇒a+d=13
⇒a=13-d …(1)
and a₄=3 ⇒a+3d=3
Putting the value of a from equation (1), we get
13-d+3d=3⇒d=-5
Putting the value of d in equation (1), we get
a=13-(-5)=18
Therefore, a₁=18 and a₃=a+(3-1)d=18+2(-5)=8

(iii) Here, a=5 and a₄=9½ to find: a₂ and a₃.
Given that: a₄=a+(4-1)d=9½
⇒5+3d=9½
3d=9½-5
d=4½÷3
d=1½
Therefore, a₂=a+d=5+1½=6½ and a₃=a+2d=5+2(1½)=8

(iv) Here, a=-4 and (16=6 to find: a₂, a₃, a₄ and a₅.
Given that: a₆=a+ (6-1)d=6

⇒-4+5d=6
5d=10
d=2
Therefore,
a₂=a+d=-4+2=-2
a₃=a+2d=-4+2(2)=0
a₄=a+3d=-4+3(2)=2
a₅=a+4d=-4+4(2)=4

(v) Here, a₂=38 and a₆=-22 to find: a₁, a₃, a₄ and a₅.
Given that: a₂=a+(2-1)d=38

⇒a+d=38
⇒a=38-d …(1)
and a₆=-22⇒a+5d=-22
Putting the value of a from equation (1), we get 38-d+5d=-22⇒d=-15
Putting the value of d in equation (1), we get
a=38-(-15)=53
Therefore,
a₁=a=53
a₃=a+2d=53+2(-15)=23
a₄=a+3d=53+3(-15)=8
a₅=a+4d=53+4(-15)=-7

Q5. Given the arithmetic sequence 1-p, 2p-3, p+5, … .
a) determine the value of p.
b) Determine the values of the first three terms of the sequence.
Solution:
a) Since this is an arithmetic sequence, you can assume that there is a common difference between the terms.

d=a₂–a₁=a₃–a₂
(2p-3)-(1-p)=(p+5)-(2p-3)
3p-4=-p+8
4p=12
p=3
p=3
b)
a₁=1-p=1-3=-2
a₂=2p-3=2(3)-3=3
a₃=p+5=3+5=8
So the first three terms of the sequence are-2, 3, 8.

Q6. Write the arithmetic progressions write first term a and common difference d are as follows:
(i) a=4, d=-3
(ii) a=-1, d=½
(iii) a=-1.5, d =-0.5
Solution:
We know that, if first term a and common difference d, then the arithmetic series is, a, a+d, a+2d, a+3d, … .
(i) a=4, d=-3
Given first term (a)=4
Common difference (d)=-3
Then arithmetic progression is, a, a+d, a+2d, a+3d, …

4, 4-3, 4+2(-3), 4+3(-3), …
4, 1,-2,-5,-8, …
a =-1, d=-½
Given,
First term (a)=-1
Common difference ((1)=1
Then arithmetic progression is,
a, a+d, a+2d, a+3d, …
-1,-1+½,-1+2⋅½,-1+3⋅½, …
-1, ½, 0, ½, ….

(iii) a=-1.5, d=-0.5
Given
First term (a)=-1.5
Common difference (d)=-0.5
hen arithmetic progression is

a, a+d, a+2d, a+3d, …
-1.5,-1.5-0.5,-1.5+2(-0.5),-1.5+3(-0.5), …
-1.5,-2,-2.5,-3, …
Then required progression is-1.5,-2,-2.5,-3, …

Q7. Determine the AP whose 3rd term is 5 and the 7th term is 9.
Solution:
We have

a₃=a+(3-1)d=a+2d=5…(1)
and a₇=a+(7-1)d=a+6d=9…(2)
Solving the pair of linear equations (1) and (2), we get a=3, d=1
Hence, the required AP is 3, 4, 5, 6, 7, …

Q8. If the sum of three numbers in an A.P., is 24 and their product is 440, find the numbers.
Solution:
Let the three numbers in A.P. be a–d, a, and a+d. According to the given information,

(a–d)+(a)+(a+d)=24…(1)
3a=24
a=8
(a–d)⋅a⋅(a+d)=440…(2)
(8-d)⋅8⋅(8+d)=440
(8-d)(8+d)=55

⇒64-d²=55
d²=64-55=9
d=±3

Therefore, when d=3, the numbers are 5, 8, and 11 and when d=-3, the numbers are 11, 8, and 5.

Q9. Determine the AP whose third term is 16 and the 7th term exceeds the 5th term by 12.
Solution:
Let the first term of the AP =a and common difference =d.
Third term =16

⇒a₃=16
a+2d=16 …(1)
7th term exceeds the 5th term by 12, therefore a₇=a₅+12
⇒a+6d=a+4d+12
2d=12 ⇒d=6
Putting the value of d in equation (1), we get a+2(6)=16
⇒a=4
Hence, the AP is a, a+d, a+2d, _ =4, 10, 16, ….

Q10. The sum of the 4th and 8th terms of an AP is 24 and the sum of the 6th and 10th terms is 44. Find the first three terms of the AP.
Solution:
Let the first term of the AP =a and common difference =d According to first condition, a₄+a₈=24

⇒a+3d+a+7d=24
2a+10d=24…(÷2)
a+5d=12
a=12-5d …(1)
According to second condition, a₆+a₁₀=44
⇒a+5d+a+9d=44
2a+14d=44
a+7d=22
Putting the value of a from equation (1), we get
(12-5d)+7d=22
2d=1
d=5
Putting the value of d in equation (1), we get a=12-5(5)=-13.
The first three terms of this AP: a, a+d, a+2d=-13,-8,-3.

Q11. A sum of $700 is to be used to give seven cash prizes to students of a school for their overall academic performance. If each prize is $20 less than its preceding prize, find the value of each of the prizes.
Solution:
Let the amount for first prize =$x
Number of prizes =7
Total prize amount =$700
Therefore, the series of 7 prizes are as follows:

(x)+(x-20)+(x-40)+(x-60)+(x-80)+(x-100)+(x-120)=700
7x-420=700
7x=1120
7x=1120÷7
x=160
Hence, the seven prizes are $160, $140, $120, $100, $80, $60 and $40.

Q12. Write down the first four terms with the following situation, will the terms be the first four terms of an arithmetic sequence?
i) The cost of digging a well for the first metre is $150 and rises by $20 for each succeeding metre.
Solution:
i) Given,
Cost of digging a well for the first meter (a₁)=$150.
Cost rises by $20 for each succeeding meter
Then,
Cost of digging for the second meter (a₂)=$150+$20=$170
Cost of digging for the third meter (a₃)=$170+$20=$210
Thus, costs of digging a well for different lengths are 150, 170, 190, 210, … .
Clearly, this series is an A.P. With first term (a)=150, common difference (d)=20