If the feasible set is not bounded
If the feasible set of a linear programming problem is not bounded (there is a direction in which you can travel indefinitely while staying in the feasible set) then a particular objective may or may not have an optimum:
▸ if it is a maximization problem, there might be a maximum, or it might be possible to make the objective arbitrarily large inside the feasible set, and
▸ if it is a minimization problem, there might be a minimum, or it might be possible to make the objective arbitrarily small (big and negative) inside the feasible set.

If there is a maximum/minimum, it can happen
▸ uniquely at a corner,
▸ at two adjacent corners and at all points in between,
▸ at a corner or along an infinite ray leaving that corner, or
▸ along an entire infinite line.

This is a little more nuanced than the Theorem stated on page (How can we Maximize an Objective Function Using Search-Line Method to the Constraints?) of the text (which is not really a true theorem ☻) …

Some unusual examples
Suppose the only constraint is y≥0. Then the feasible set is unbounded and has no corners.
▸ Objective =y has no maximum. It has a minimum, reached along the entire x-axis.
▸ Objective =-y has no minimum, but has a maximum
▸ Objective =x–y has no minimum, and no maximum
Suppose the constraints are y≥0 and x≥0. Then the
feasible set is unbounded and has one corner.
▸ Objective =x+y has a minimum, reached uniquely at the corner.
▸ Objective =y has a minimum, reached along the ray starting at the corner and moving to the right.
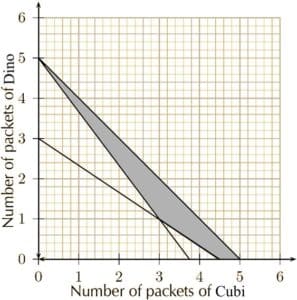
Suppose the constraints are y≥0, x≥0, y≤2. Then the feasible set is unbounded and has two corners.
▸ Objective =x has a minimum, reached at both corners, and between the two corners.

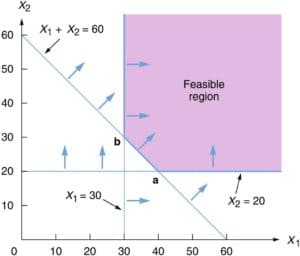
📌 Example 1. Maximize z=2x+y subject to 3x+y≥6, x+y≥4, x≥0, and y≥0.
✍

Since the feasible region is unbounded there may be no maximum value of z.
For x≥4, (x,0) is a feasible solution.
At (x,0), z=2x.
Therefore as x increases without bound, z increases without bound and there is no maximum value ofz.

📌 Example 2. Determine the minimum value of Z=3x+2y (if any), if the feasible region for an LPP is shown in Fig.LP.1.
Solution:
The feasible region (R) is unbounded. Therefore minimum of Z may or may not exist. If it exists, it will be at the corner point (Fig.LP.1).

Corner Point	Value of Z
A(12,0) B(4,2) C(1,5) D(0,10)	3⋅12+2⋅0=36 3⋅4+2⋅2=16 3⋅1+2⋅5=13← smallest 3⋅0+2⋅10=20

(Fig.LP.1)

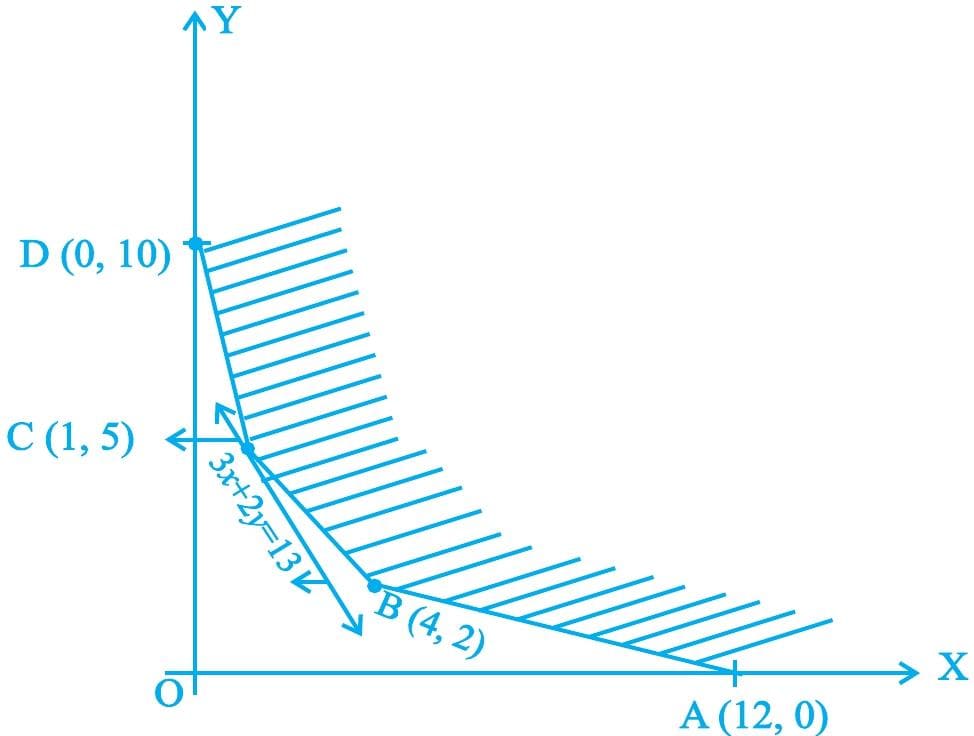
Let us graph 3x+2y<13. We see that the open half plane determined by 3x+2y<13 and R do not have a common point. So, the smallest value 13 is the minimum value of Z.

📌 Ex3. Minimize Z=3x+5y
such that x+3y≥3, x+y≥2, x,y≥0.
✍
The feasible region determined by the system of constraints, x+3y≥3, x+y≥2, x,y≥0, is as follows.

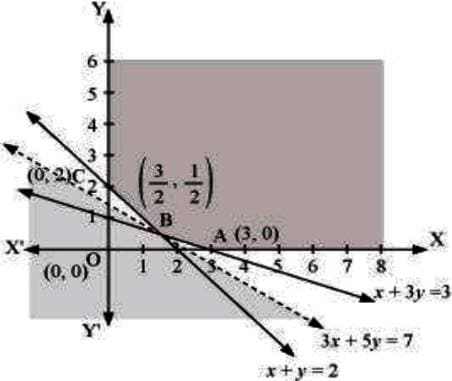
It can be seen that the feasible region is unbounded.
The corner points of the feasible region are A(3, 0), B(1½, ½), and C(0, 2).
The values of 2 at these corner points are as follows.

Corner point	Z=3x+5y
A(3, 0)	9 B(1½, ½)	7→Smallest C(0,2)	10

As the feasible region is unbounded, therefore, 7 may or may not be the minimum value of Z.
For this, we draw the graph of the inequality, 3x+5y<7, and check whether the resulting half plane has points in common with the feasible region or not. It can be seen that the feasible region has no common point with 3x+5y<7. Therefore, the minimum value of Z is 7 at (1½, ½).

📌 Ex4. Maximize Z=-x+2y, subject to the constraints:

x≥3, x+y≥5, x+2y≥6, y≥0.
✍
The feasible region determined by the constraints, x≥3, x+y≥5, x+2y≥6, and y≥0 is as follows.

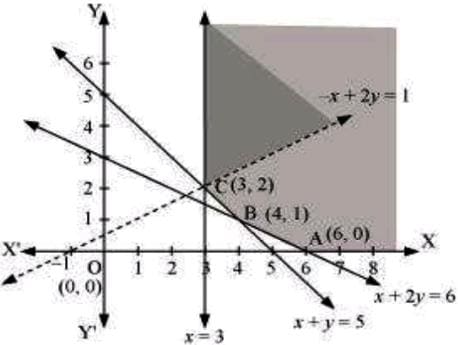
It can be seen that the feasible region is unbounded.
The values of Z at corner points A(6, 0), B(4, 1), and C(3, 2) are as follows.

Corner point	Z=x+2y
A(6, 0)	Z=-6 B(4, 1)	Z=-2 C(3, 2)	Z=1

As the feasible region is unbounded, therefore, Z=1 may or may not be the maximum value.
For this, we graph the inequality, –x+2y>1, and check whether the resulting half plane has points in common with the feasible region or not.
The resulting feasible region has points in common with the feasible region.
Therefore, Z=1 is not the maximum value. Z has no maximum value.

📌 Ex5. Maximize Z=x+y, subject to x–y≤-1, –x+y≤0, x,y≥0.
✍
The region detennined by the constraints, x–y≤-1, –x+y≤0, x,y≥0, is as follows.

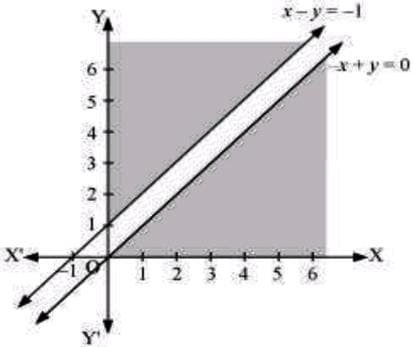
There is no feasible region and thus, Z has no maximum value.

📌 Ex6. Determine graphically the minimum value of the objective function

Z=-50x+20y … (1)
subject to the constraints:
2x–y≥-5 … (2)
3x+y≥3 … (3)
2x-3y≤12 … (4)
x≥0,y≥0 … (5)
Solution:
First of all, let us graph the feasible region of the system of inequalities (2) to (5). The feasible region (shaded) is shown in the Fig.LP.2. Observe that the feasible region is unbounded.

[Fig.LP.2]
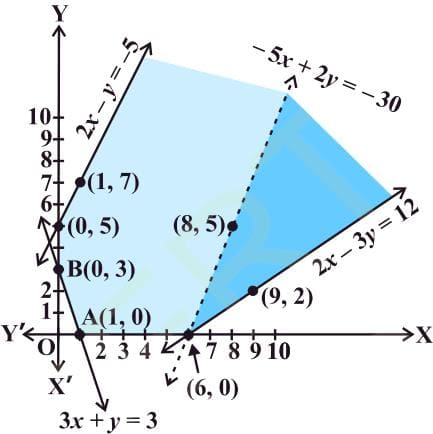
We now evaluate Z at the corner points.

Corner Point	Z=-50x+20y
(0, 5) (0, 3) (1, 0) (6, 0)	100 60 -50 -300 ← smallest

From this table, we find that — 300 is the smallest value of Z at the corner point (6, 0). Can we say that minimum value of Z is — 300? Note that if the region would have been bounded, this smallest value of Z is the minimum value of Z (Theorem 2). But here we see that the feasible region is unbounded. Therefore, — 300 may or may not be the minimum value of Z. To decide this issue, we graph the inequality

-50x+20y<-300 … (÷3) -5x+2y<-30
and check whether the resulting open half plane has points in common with feasible region or not. If it has common points, then -300 will not be the minimum value of Z. Otherwise, -300 will be the minimum value of Z.

As shown in the Fig.LP.2, it has common points. Therefore, Z=-50 x+20y has no minimum value subject to the given constraints.

In the above example, can you say whether z=-50 x+20y has the maximum value 100 at (0, 5)? For this, check whether the graph of -50x+20y>100 has points in common with the feasible region.

📌 Ex7: An Unbounded Region
Find the maximum value of

z=4x+2y [Objective function]
where x≥0 and y≥0 subject to the constraints

x+2y≥4 3x+y≥7 –x+2y≤7.

}Constraints

Solution:
The region determined by the constraints is shown below.

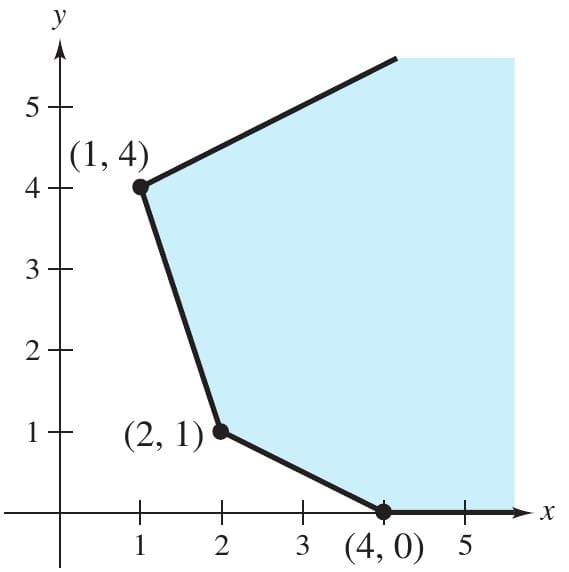
For this unbounded region, there is no maximum value ofz. To see this, note that the point (x,0) lies in the region for all values of x≥4. By choosing large values of x, you can obtain values of
z=4(x)+2(0)=4x
that are large. So, there is no maximum value ofz.

Remark:
For this problem, the objective function does have a minimum value, z=10, which occurs at the vertex (2, 1).