📌 Question 1. A manufacturing company makes two types of television sets; one is black and white and the other is colour. The company has resources to make at most 300 sets a week. It takes $1800 to make a black and white set and $2700 to make a coloured set. The company can spend not more than $648,000 a week to make television sets. If it makes a profit of $510 per black and white set and $675 per coloured set, how many sets of each type should be produced so that the company has maximum profit? Formulate this problem as a LPP given that the objective is to maximize the profit.
✍ Solution:
Let x and y denote, respectively, the number of black and white sets and coloured sets made each week. Thus

x≥0, y≥0.
Since the company can make at most 300 sets a week, therefore,
x+y≤300.
Weekly cost (in $) of manufacturing the set is
1800x+2700y
and the company can spend upto $648,000. Therefore,
1800x+2700y≤648,000, i.e., or 2x+3y≤720
The total profit on x black and white sets and y colour sets is $(510x+675y). Let Z=510x+675y. This is the objective function.

Thus, the mathematical formulation of the problem is maximizing Z=510x+675y subject to the constraints:

x+y≤300;2x+3y≤720;x≥0;y≥0.

Figure LP1
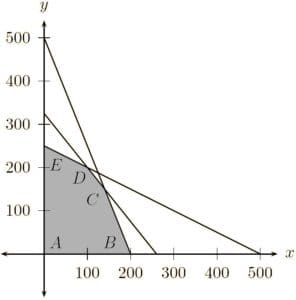
The feasible region OABC is shown in the Figure LP1.
Since the feasible region is bounded, therefore maximum of Z must occur at the corner point of OBC.

Corner Point	Value of Z
O(0, 0)	510(0)+675(0)=0
A(300, 0)	510(300)+675(0)=153000
B(180, 120)	510(180)+675(120)=178200←maximum
C(0, 240)	510(0)+675(240)=162000

Thus, maximum Z is 172800 at the point (180, 120), i.e., the company should produce 180 black and white television sets and 120 coloured television sets to get maximum profit.

📌 Question 2. A factory makes tennis rackets and cricket bats. A tennis racket takes 1.5 hours of machine time and 3 hours of craftsman’s time in its making while a cricket bat takes 3 hour of machine time and 1 hour of craftsman’s time. In a day, the factory has the availability of not more than 42 hours of machine time and 24 hours of craftsman’s time.
(i) What number of rackets and bats must be made if the factory is to work at full capacity?
(ii) If the profit on a racket and on a bat is $20 and $10 respectively, find the maximum profit of the factory when it works at full capacity.
✍ Solution:
(i) Let the number of rackets and the number of bats to be made be x and y respectively.
The machine time is not available for more than 42 hours.

∴1.5x+3y≤42…(1)
The craftsman’s time is not available for more than 24 hours.
∴3x+y≤24…(2)
The factory is to work at full capacity. Therefore,
1.5x+3y=42
3x+y=24
On solving these equations, we obtain x=4 and y=12.
Thus, 4 rackets and 12 bats must be made.
(ii) The given information can be complied in a table as follows:

	Tennis Racket	Cricket Bat	Availability
Machine Time (h)	1.5	3	42
Craftsman’s Time (h)	3	1	24

1.5x+3y≤42
3x+y≤24
x,y≥0
The profit on a racket is $20 and on a bat is $10.
∴Z=20x+10y
The mathematical formulation of the given problem is
Maximize Z=20x+10y … (1)
subject to the constraints, 1.5x+3y≤42 … (2)
3x+y≤24 … (3)
x,y≥O … (4)
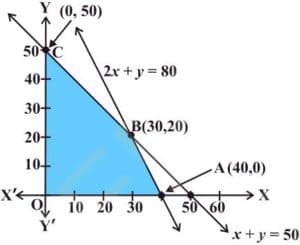
The feasible region determined by the system of constraints is as follows:

The corner points are A(8, 0), B(4, 12), C(0, 14), and O(0, 0).
The values of Z at these corner points are as follows:

Corner point	Z=20x+10y
A(8, 0)	160
B(4, 12)	200	→ Maximum
C(0, 14)	140
D(0, 0)	0

Thus, the maximum profit of the factory when it works to its full capacity is $200.

📌 Question 3. A manufacturer produces nuts and bolts. It takes 1 hour of work on machine A and 3 hours on machine B to produce a package of nuts. It takes 3 hours on machine A and 1 hour on machine B to produce a package of bolts. He earns a profit, of $17.50 per package on nuts and $7.00 per package on bolts. How many packages of each should be produced each day so as to maximize his profit, if he operates his machines for at the most 12 hours a day?
✍ Solution:
Let the manufacturer produce x packages of nuts and y packages of bolts. Therefore, x≥0 and y≥0.
The given information can be compiled in a table as follows:

	Nuts	Bolts	Availability
Machine A (h)	1	3	12
Machine B (h)	3	1	12

The profit on a package of nuts is $17.50 and on a package of bolts is $7. Therefore, the constraints are

x+3y≤12
3x+y≤12
Total profit, Z=17.5x+7y.
The mathematical formulation of the given problem is
Maximize Z=17.5x+7y…(1)
subject to the constraints,
x+3y≤12…(2)
3x+y≤12…(3)
x,y≥⋯(4)
The feasible region determined by the system of constraints is as follows:

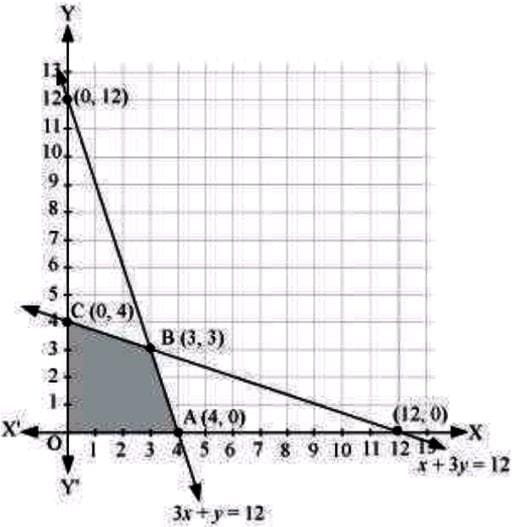
The corner points are A(4, 0), B(3, 3), and C(0, 4). The values of Z at these corner points are as follows:

Corner point	Z=17.5x+7y
O(0, 0)	0
A(4, 0)	70
B(3, 3)	73.5	→ Maximum
C(0, 4)	28

The maximum value of Z is $73.50 at (3, 3).
Thus, 3 packages of nuts and 3 packages of bolts should be produced each day to get the maximum profit of $73.50.

📌 Question 4. A factory manufactures two types of screws, A and B. Each type of screw requires the use of two machines, an automatic and a hand operated. It takes 4 minutes on the automatic and 6 minutes on hand operated machines to manufacture a package of screws A, while it takes 6 minutes on automatic and 3 minutes on the hand operated machines to manufacture a package of screws B. Each machine is available for at the most 4 hours on any day. The manufacturer can sell a package of screws A at a profit of $7 and screws B at a profit of $10. Assuming that he can sell all the screws he manufactures, how many packages of each type should the factory owner produce in a day in order to maximize his profit? Determine the maximum profit.
✍ Solution:
Let the factory manufacture x screws of type A and y screws of type B on each day. Therefore, x≥0 and y≥0.
The given information can be compiled in a table as follows:

	Screw A	Screw B	Availability
Automatic Machine (min)	4	6	4×60=240
Hand Operated Machine (min)	6	3	4×60=240

The profit on a package of screws A is $7 and on the package of screws B is $10. Therefore, the constraints are

4x+6y≤240
6x+3y≤240
Total profit, Z=7x+10y
The mathematical formulation of the given problem is
Maximize Z=7x+10y…(1)
subject to the constraints,
4x+6y≤240…(2)
6x+3y≤240…(3)
x,y≥0…(4).
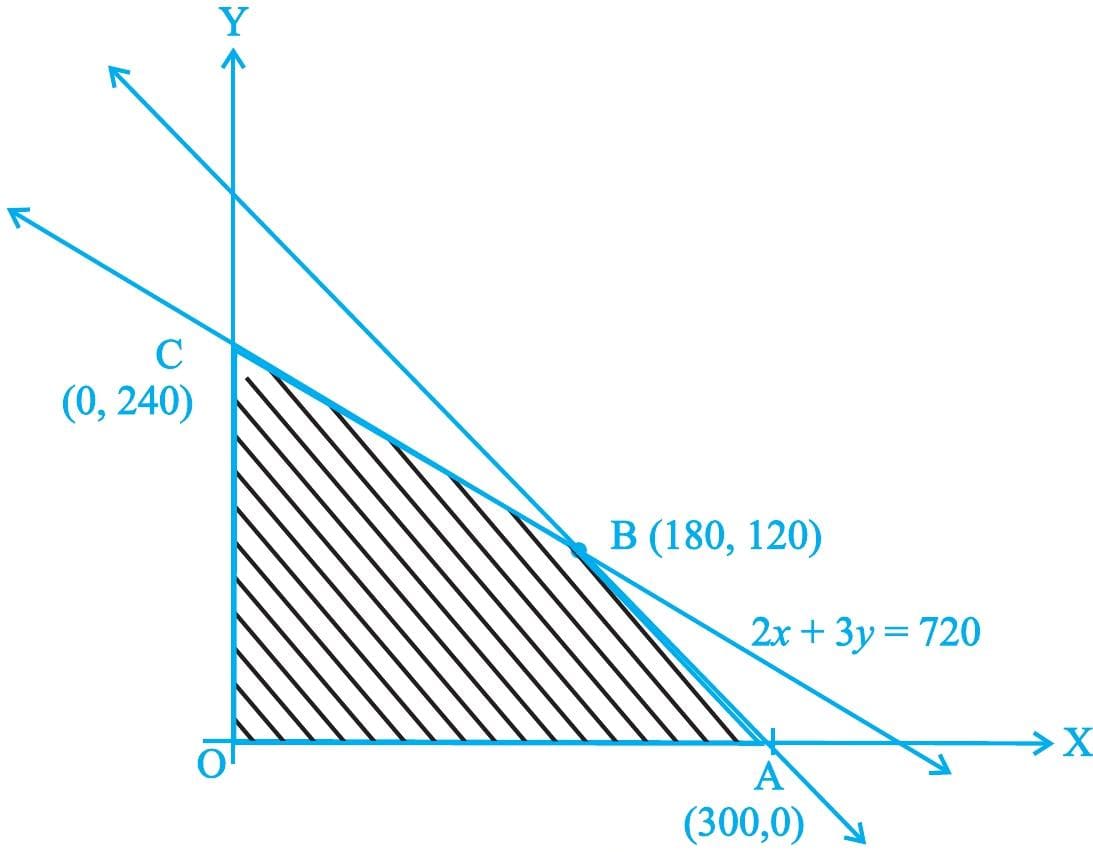
The feasible region determined by the system of constraints is

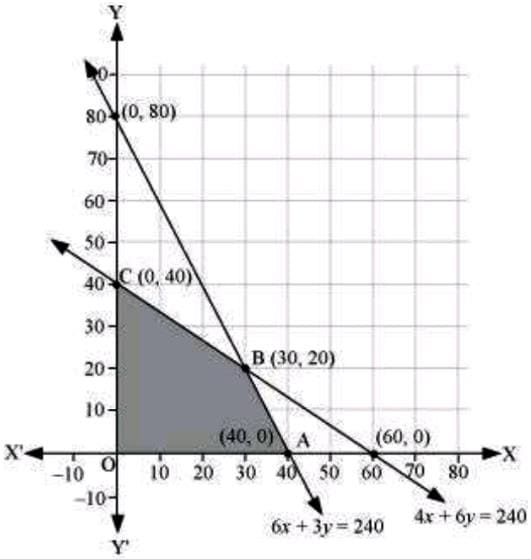
The corner points are A(40, 0), B(30, 20), and C(0, 40).
The values of Z at these corner points are as follows:

Corner point	Z=7x+10y
A(40, 0)	280
B(30, 20)	410	→ Maximum
C(0, 40)	400

The maximum value of Z is 410 at (30, 20).
Thus, the factory should produce 30 packages of screws A and 20 packages of screws B to get the maximum profit of $410.

📌 Question 5. A cottage industry manufactures pedestal lamps and wooden shades, each requiring the use of a grinding/cutting machine and a sprayer. It takes 2 hours on grinding/cutting machine and 3 hours on the sprayer to manufacture a pedestal lamp. It takes 1 hour on the grinding/cutting machine and 2 hours on the sprayer to manufacture a shade. On any day, the sprayer is available for at the most 20 hours and the grinding/cutting machine for at the most 12 hours. The profit from the sale of a lamp is $5 and that from a shade is $3. Assuming that the manufacturer can sell all the lamps and shades that he produces, how should he schedule his daily production in order to maximize his profit?
✍ Solution:
Let the cottage industry manufacture x pedestal lamps and y wooden shades. Therefore, x≥0 and y≥0.
The given information can be compiled in a table as follows:

	Lamps	Shades	Availability
Grinding/Cutting Machine (h)	2	1	12
Sprayer (h)	3	2	20

2x+y≤12
3x+2y≤20
Total profit, Z=5x+3y.
The mathematical formulation of the given problem is maximizing Z=5x+3y…(1)
subject to the constraints,
2x+y≤12…(2)
3x+2y≤20…(3)
x,y≥0…(4)
The feasible region determined by the system of constraints is as follows:

The corner points are A(6, 0), B(4, 4), and C(0, 10).
The values of Z at these corner points are as follows:

Corner point	Z=5x+3y
A(6, 0)	30
B(4, 4)	32	→ Maximum
C(0, 10)	30

The maximum value of Z is 32 at (4, 4).
Thus, the manufacturer should produce 4 pedestal lamps and 4 wooden shades to maximize his profits.

📌 Question 6. A company manufactures two types of novelty souvenirs made of plywood. Souvenirs of type A require 5 minutes each for cutting and 10 minutes each for assembling. Souvenirs of type B require 8 minutes each for cutting and 8 minutes each for assembling. There are 3 hours 20 minutes available for cutting and 4 hours of assembling. The profit is $5 each for type A and $6 each for type B souvenirs. How many souvenirs of each type should the company manufacture in order to maximize the profit?
✍ Solution:
Let the company manufacture x souvenirs of type A and y souvenirs of type B.
Therefore, x≥0 and y≥0.
The given information can be complied in a table as follows:

	Type A	Type B	Availability
Cutting (min.)	5	8	3⋅60+20=200
Assembling (min.)	10	8	4⋅60=240

The profit on type A souvenirs is $5 and on type B souvenirs is $6. Therefore, the constraints are

5x+8y≤200
10x+8y≤240…(÷2)→5x+4y≤120
Total profit, Z=5x+6y.
The mathematical formulation of the given problem is maximizing Z=5x+6y … (1)
subject to the constraints,
5x+8y≤200…(2)
5x+4y≤120…(3)
x,y≥0…(4)
The feasible region determined by the system of constraints is as follows:

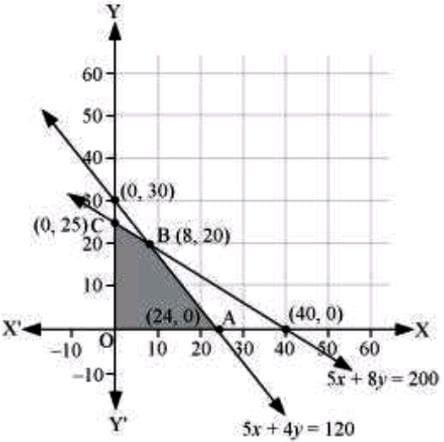
The corner points are A(24, 0), B(8, 20), and C(0, 25).
The values of Z at these corner points are as follows:

Corner point	Z=5x+6y
A(24, 0)	120
B(8, 20)	160	→ Maximum
C(0, 25)	150

The maximum value of Z is 200 at (8, 20).
Thus, 8 souvenirs of type A and 20 souvenirs of type B should be produced each day to get the maximum profit of $160.

📌 Question 7. A manufacturer makes two types of toys A and B. Three machines are needed for this purpose and the time (in minutes) required for each toy on the machines is given below:

Type of toys	Machines
	I	II	III
A	12	18	6
B	6	0	9

Each machine is available for a maximum of 6 hours per day. If the profit on each toy of type A is $7.50 and that on each toy of type B is $5, show that 15 toys of type A and 30 of type B should be manufactured in a day to get maximum profit.
✍ Solution:
Let x and y toys of type A and type B respectively be manufactured in a clay.
The given problem can be formulated as follows:
Maximize z=7.5x+5y … (1)
subject to the constraints,

2x+y≤60…(2)
x≤20…(3)
2x+3y≤120…(4)
x,y≥0…(5)
The feasible region determined by the constraints is as follows:

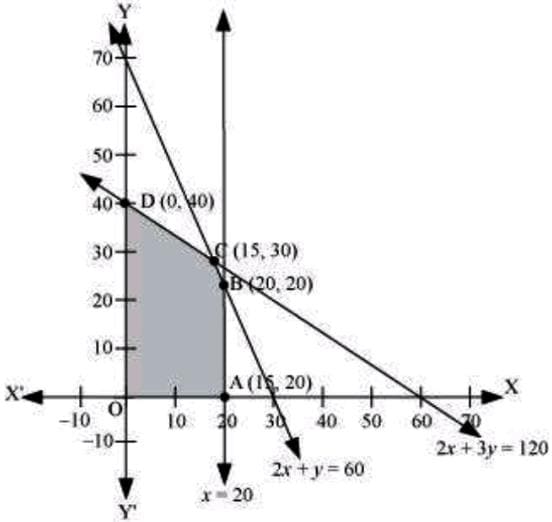
The corner points of the feasible region are A(20, 0), B(20, 20), C(15, 30), and D(0, 40). The values of 2 at these corner points are as follows:

Corner point	z=7.5x+5y
A(20, 0)	150
B(20, 20)	250
C(15, 30)	262.5	→ Maximum
D(0, 40)	200

The maximum value of z is 262.5 at (15, 30).
Thus, the manufacturer should manufacture 15 toys of type A and 30 toys of type B to maximize the profit.

📌 Question 8. A toy company manufactures two types of dolls, A and B. Market tests and available resources have indicated that the combined production level should not exceed 1200 dolls per week and the demand for dolls of type B is at most half of that for dolls of type A. Further, the production level of dolls of type A can exceed three times the production of dolls of other type by at most 600 units. If the company makes profit of $12 and $16 per doll respectively on dolls A and B, how many of each should be produced weekly in order to maximize the profit?
Answer
Let x and y be the number of dolls of type A and B respectively that are produced per week.
The given problem can be formulated as follows:
Maximize z=12x+16y…(1)
subject to the constraints,

x+y≤1200…(2)
y≤½x→x≥2y…(3)
x-3y≤600…(4)
x,y≥0…(5)
The feasible region determined by the system of constraints is as follows:

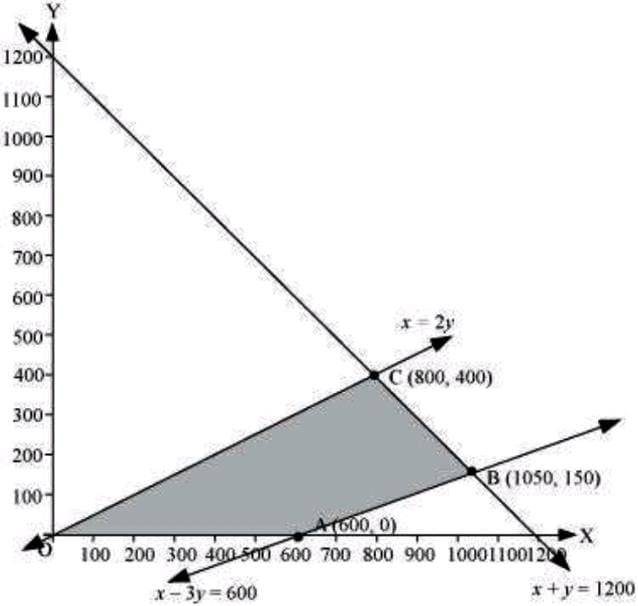
The corner points are A(600, 0), B(1050, 150), and C(800, 400).
The values of z at these corner points are as follows:

Corner point	z=12x+16y
A(600, 0)	7200
B(1050, 150)	15000
C(800, 400)	16000	→ Maximum

The maximum value of z is 16000 at (800, 400). Thus, 800 and 400 dolls of type A and type B should be produced respectively to get the maximum profit of $16000.