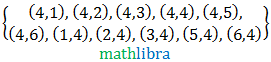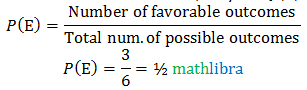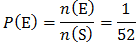Sample space consists of expected elements and not expected elements of an event. In other words, sample space contains favorable outcomes and the outcomes of complement of an event.
Events like throwing dice at a time, toss coins twice, withdrawing cards from a deck of 52 cards, pick balls at a time and others.

Examples and Solutions

Ex1. In how many ways, a cookie flavor can be selected from 5 types of fruits; wherein a flavour can be a combination of any number of fruits?
A. 120 B. 32 C 31 D. 5
correct: C, solution:
A fruit can be added or not added to form a flavor. Hence the total number of flavors that can be made by using 5 fruits =2⁵-1=31. (Since a flavor with no fruit cannot be made).

Ex2. In how many ways letters of the word UNION can be arranges such that N’s are not together?
A.36 B.24 C.84 D.60
correct: A, solution:
Let us first calculate the total number of possible words using these alphabets and then we will subtract the cases where N’s are together.
There are 2 letters of N causes that the total number of possible words is calculated by ‘the number of arrangements with kinds of alike elements’.
Total number of possible words

Ex3. How many distinct colors can be formed with the help of 7 different colors by mixing any number of colors in equal quantity?
A. 128 B. 127 C. 28 D. 56
correct: B, solution:
There is a choice of adding or not adding a particular color with each of the color. Number of distinct colors by mixing 2 colors, 3, 4, 5, 6, 7 ones is equal to 2⁷ ways which also includes not mixing any of the color. So total number of distinct colors that can be made =128-1=127.

Ex4. During a war, certain codes are generated by flashing certain number of flags of different colours. There are total of 5 colours of flags which can be used for flashing. How many different codes can be generated with the help of these flags? Assume that sequence of the flashing the flags will not be considered as different signals.
a.32 b.31 c. 120 d. 30
correct: b, solution:
Each flag can be used or cannot be used for flashing signals. Hence, there are two ways a flag can be used for signaling. Total number of ways 2⁵-1=31 (since 0 flags cannot be used for signaling).

Ex5. In how many ways. at least one fruit can be selected from 6 types of fruits if 4 fruits of each type are available for selection?
A. 5⁶-1 B. 6⁴-1
C. 4⁶-1 D. 6⁵-1
correct: A, solution:
Number of possible selections out of every type of fruit is 5.
Hence, total number of possible selections are 5⁶. But, since at least one fruit is to be selected, number of ways will be 5⁶-1.

Ex6. There are 15 points on a piece of paper out of which 5 points are collinear and no other three points are collinear. Find the number of distinct triangles that can be formed by joining these points.
A. 455 B. 435 C. 445 D. 425
correct: C, solution:
Number of triangles that can be formed from 15 points
is ¹⁵C₃. Since there are 5 collinear points so ⁵C₃ triangles cannot be formed. So total no of triangles that can be formed =455-10=445

Ex7. There are 15 points on a piece of paper. 5 out of these 15 points are collinear and no other 3 points are collinear. Find the number of distinct lines that can be drawn on this paper by joining any pair of points
A. 90 B. 91 C. 105 D. 96
correct: D, solution:
From 15 points ¹⁵C₂ lines can be drawn. There are 5 collinear points so ⁵C₂ lines will give rise to a single line. So there will be ¹⁵C₂–⁵C₂+1=96 distinct lines.

Ex8. Find the number of three digit numbers which contain 5 as at least one of the digits
A 252 B. 255 C. 258 D. 261
correct: A, solution:
The simplest way to do is to find the numbers with no 5 in it and subtract it from the total number of 3 digit numbers The number of digits that can be placed at the places are