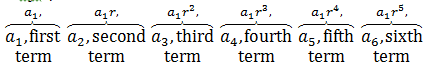General Equation for the nth-term of a Geometric Sequence
From the above example we know a₁=2 and r=2, and we have seen from the table that the nth-term is given by a_n=2×2^(n-1). Thus, in general,

a_n=a₁⋅r^(n-1)
where a₁ is the first term and r is called the common ratio.

So, if we want to know how many people are newly-infected after 10 days, we need to work out a₁₀.

a_n=a₁⋅r^(n-1)
a₁₀=2⋅r^(10-1)
2×2⁹=2×512=1024.
That is, after 10 days, there are 1024 newly-infected people.
Or, how many days would pass before 16, 384 people become newly infected with the flu virus?
a_n=a₁⋅r^(n-1)
16, 384=2⋅2^(n-1)
16, 384÷2=2^(n-1)
8 192=2^(n-1)
2¹³=2^(n-1)
13=n-1
n=14.
That is, 14 days pass before 16, 384 people are newly-infected.

📌 Example 1. Determine the number of terms in the sequence: 2, 4, 8, …, 1024.
✍ Solution:

a=2, r=4/2=8/4=2
a⋅r^(n-1)=1024
2⋅2^(n-1)=2¹⁰→2ⁿ=2¹⁰
n=10

📌 Ex2. Find n in the geometric sequence 4, -2, 1, …. if a_n=1/16
✍ Solution:
Since 4, -2, 1, …
Here, a=4, r=-2÷4=-½, a_n=1/16

a_n=a⋅r^(n-1)
1/16=4⋅(-½)^(n-1)
1/64=(-½)^(n-1)
(-½)⁶=(-½)^(n-1)
6=n-1→n=7.

We can also check whether a given number belongs to a given geometric sequence.
📌 Question 1. Does the number 48 belong to the geometric sequence

3072, 1536, 768, …?
✍ Solution:
Here a=3072 and r=½, so a_n=3072×½^(n-1).
We set 3072×½^(n-1)=48. This gives ½^(n-1)=1/64, that is, 2^(n-1)=64=2⁶, and so n=7.
Hence, 48 is the 7th term of the sequence.

📌 Q2. Does the number 6072 belong to the geometric sequence

3, -6, 12, -24, 48, …?
✍ Solution:
Here a=3 and r=-2, so a_n=3×(-2)^(n-1).
We set 3×(-2)^(n-1)=6072. This gives (-2)^(n-1)=2024.
But 2024 is not a power of 2, and so 6072 does not belong to the sequence.

If given a sequence then check whether it is either arithmetic, geometric or quadratic.

📌 Q3. Given the sequence 1, ⅔, 9/4, ….
a) Determine the next two terms
b) Which term of the sequence is equal to 32/243?
✍ Solution:
The common ratio ⅔ because ⅔÷1=⅔=4/9÷⅔
a) a₄=a⋅r³=1⋅⅔³=8/27 and a₅=a⋅r⁴=1⋅⅔⁴=16/81
b) a=1, r=⅔ and a_n=a⋅r^(n-1)=32/243

=1⋅⅔⁵
n-1=5
n=6.

📌 Q4: Which term of the geometric sequence., 2, 8, 32, up to n terms is 131072?
✍ Solution: Let 131072 be the nth term of the given geometric sequence. Here a=2 and r=4. Therefore 131072=a_n=2⋅4^(n-1) or 65536=4^(n-1)
This gives 4⁸=4^(n-1)
So that n-1=8, ie, n=9. Hence, 131072 is the 9th term of the geometric sequence.

📌 Questions:
(a) What term number is 128 of the sequence 2, 2√2, 4, …?
(b) What term number is 729 of the sequence √3, 3, 3√3, …?
(c) What term number is 1/19683 of the sequence ⅓, 1/9, 1/27, …?
✍ Solutions:
(a) a₁=(√2)²; a₂=(√2)³; a₃=(√2)⁴; a_n=(√2)⁽ⁿ⁺¹⁾

128=2⁷=(√2)^(2×7)=(√2)⁽¹³⁺¹⁾=a₁₃
Thus, 128 is the 13th term of the given sequence.
(b) a₁=(√3)¹; a₂=(√3)²; a₃=(√3)³; a_n=(√3)ⁿ
729=3⁶=(√3)^(2×6)=(√2)¹²=a₁₂
Thus, 729 is the 12th term of the given sequence.
(c)
a₁=⅓¹; a₂=⅓²; a₃=⅓³; a_n=⅓ⁿ
1/19683=⅓⁹=a₉.
Thus, 1/19683 is the 9th term of the given sequence.