A coin has two sides, Head and Tail. If an event consists of more than one coin, then coins are considered as. distinct, if not otherwise stated.

Tossing a coin once

📌 Ex1. A coin is tossed once. Find the probability of:
(i) getting a tail
(ii) not getting a tail
✍ Solution:
Sample Space ={H,T}

n(S)=2
(i) A= Event of getting a tail ={T}
n(A)=1
Therefore. the probability of getting a tail =
n(A)/n(S)=½
(ii) Not getting a tail means getting a head.
Event of getting a head ={H}
n(A)=1
Therefore, the probability of getting a tail =
n(A)=1

📌 Ex2. Why is tossing a coin considered to be a fair way of deciding which team should choose ends in a game of cricket?
✍ Solution:
Number of possible outcomes while tossing a coin =2 (1 head & 1 tail)

P(getting head)=½
P(getting tail)=½
Since probability of two events are equal, these are called equally like events.
Hence, tossing a coin is considered to be a fair way of deciding which team should choose ends in a game of cricket.

📌 Ex3. Brian tossed an unbiased coin ten times and in all the results he got head (weird, just example). What is the probability of getting a head in his next toss?
a. 1 b. ½ c. 1⁄11 d. 10/11
✍ correct: b, solution:
This case is also called as a condititional probability that we shall study it.
As 11th toss is independent event so probability of getting a head =½.

Tossing a coin twice

📌 Ex4. A coin is tossed twice, what is the probability that atleast one tail occurs?
✍ Solution:
When a coin is tossed twice, the sample space is given by

S={HH,HT,TH,TT}
Let A be the event of the occurrence of at least one tail.
Accordingly, A={HT,TH,TT}

Tossing two coins once

📌 Ex5. Two coins are tossed, find the probability that two heads are obtained.
Note: Each coin has two possible outcomes H (heads) and T (Tails).
✍ Solution:
The sample space S is given by.

S={(H,H),(H,T),(T,H),(T,T)}
Let E be the event “two heads are obtained”.
S={(H,H)}
We use the formula of the classical probability.
P(E)=n(E)/n(S)=¼

📌 Ex6. Two coins are tossed, find the probability that one head only is obtained.
✍ Solution:
Each coin has two possible outcomes H (heads) and T (Tails).
S={HH,HT,TH,TT};E={HT,TH};n(S)=4;n(E)=2
P(E)=n(E)/n(S) =2/4=½

📌 Ex7. Harpreet tosses two different coins simultaneously (say, one is of a 1 cent and other of a 2 cent).
What is the probability that he gets at least one head?
✍ Solution:
Total number of possible outcomes n(S)=4 which are

{HT,HH,TT,TH}
E→ event of getting at least one head {HT,HH,TH}, n(E)=3
P(E)=¾

📌 Ex8. If two coins are tossed once, what is the probability of getting:
(i) both heads.
(ii) at least one head.
(iii) both heads or both tails.
✍ Solution:
When two coins are tossed together possible number of outcomes ={HH,TH,HT,TT};n(S)=4.
(i) E= event of getting both heads ={HH};n(S)=1
Probability of getting both heads =n(E)/n(S)=¼
(ii) E= event of getting at least one head

={HH,TH,HT};n(E)=3
Probability of getting at least one head =n(E)/n(S)=¾
(iii) E= event of getting both heads or both tails
={HH,TT};n(E)=2
Probability of getting both heads or both tails =n(E)/n(S)=½

📌 Ex9. Harpreet tosses two different coins simultaneously (say, one is of a 1 cent and other of a 2 cent). What is the probability that she gets at least one head?
✍ Solution:
We write H for ‘head’ and T for ‘tail’. When two coins are tossed simultaneously, the possible outcomes are (H, H), (H, T), (T, H), (T, T), which are all equally likely.
Here (H, H) means head up on the first coin (say on Re 1) and head up on the second coin (Rs 2). Similarly (H, T) means head up on the first coin and tail up on the second coin and so on.
The outcomes favorable to the event E, ‘at least one head’ are (H, H), (H, T) and (T, H). So, the number of outcomes favorable to E is 3.
Therefore, P(E)=¾. The probability that Harpreet gets at least one head is ¾.

Tossing a coin three times

📌 Ex10. Experiment:
A fair coin is tossed three times. Find the probability in each case: It shows events Happening:
(i). One tail
✍ Solution:
Sample space,

S={HHH,HHT,HTH,HTT,THH,THT,TTH,TTT}
n(S)=8
Let event A denote the occurrence of one tail, then
P(A)=n(A)/n(S)=⅜
(ii). Atleast one head
✍ Solution:
Let event B denote the occurrence of atleast one head, then
P(B)=n(B)/n(S)=⅞

📌 Ex11. A game consists of tossing a one cent coin 3 times and noting its outcome each time. Alan wins if all the tosses give the same result i.e., three heads or three tails, and loses otherwise. Calculate the probability that Alan will lose the game.
✍ Solution:
The possible outcomes are

{HHH,TTT,HHT,HTH,THH,TTH,THT,HTT}
Number of total possible outcomes =8
Number of favorable outcomes =2 {i.e., HHH and TTT }
P(Alan will win the game)=2/8=
P(Alan will lose the game)=1-¼=¾

Tossing three coins once

📌 Ex12. Three coins are tossed and the number of heads is observed.
(a) List the sample space for this experiment.
(b) Find the probabilities of each element of the sample space.
(c) If A is the event that at least one head appears, find P(A).
(d) If B is the event that all heads or all tails appear, find P(B).
✍ Solution:
(a) S={HHH,HHT,HTH,HTT,THH,THT,TTH,TTT}
(b) n(S)=8;P=⅛
(c) E={HHH,HHT,HTH,HTT,THH,THT,TTH}
P(E)=⅞
(d) E={HHH,TTT};P(E)=¼

📌 Ex13. Three coins are tossed together. Write all the possible outcomes. Now, find the probability of getting:
(i) all tails (ii) 3 tails (iii) no heads (iv) 3 heads (v) no tails (vi) exactly two tails (vii) exactly two heads (viii) at least one tail (ix) at least one head and one tail (x) at least two heads (xi) at most two heads (xii) atmost two tails
✍ Solution:
When three coins are tossed once, the sample space is given by

S={HHH,HHT,HTH,THH,HTT,THT,TTH,TTT}
∴ Accordingly, n(S)=8
It is known that the probability of an event E is given by

(i) Favorable outcomes for all tails ={TTT}
Number of favorable outcomes =1
P(all tails)=⅛ as same as P(3 tails) and P(no heads).
Hence, (i), (ii), (iii) are same meaning.
(iv) The expected outcome is only {HHH}.
P(3 heads)=⅛ as same as P(no tails).
Hence, both (iv), (v) are same meaning.
(vi). Let A be the event of the occurrence of exactly two tails.
Accordingly, A={HTT,THT,TTH}
P(A)=n(A)/n(S)→P(A)=⅜
(vii) Let B be the event of the occurrence of 2 heads. Accordingly, B={HHT,HTH,THH}
P(B)=⅜
(viii) Favorable outcomes for at least one tail
S={HHT,THH,HTH,HTT,THT,TTH,TTT}
Number of favorable outcomes =7
P(at least one tail)=⅞
(ix) C→ getting at least one head & one tail
Exclude {(HHH,TTT)} from the possible outcomes.
P(C)=(8-2)/8=¾
(x). Let D be the event of the occurrence of at least 2 heads. Accordingly, D={HHH,HHT,HTH,THH}
P(D)=4/8=½
(xi) Let E be the event of the occurrence of at most 2 heads. Accordingly,
E={HHT,HTH,THH,HTT,THT,TTH,TTT};n(E)=7
P(E)=n(E)/n(S) →P(E)=⅞
(xii). Let F be the event of the occurrence of at most 2 tails.
Accordingly, F={HHH,HHT,HTH,THH,HIT,THT,TTH}
P(J)=n(J)/n(S) →P(J)=⅞

Tossing a coin several times

📌 Ex14. A coin is tossed four times. Find the probability in each case: The tops show event happening:
(i). All heads
✍ Solution:

n(S)=16
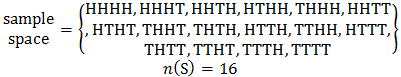
Let event A denote that the top shows all heads. So
n(A)=1
P(A)=n(A)/n(S) =1/16
(ii). 2 heads and 2 tails
✍ Solution:
Let event B denote that the top shows all heads. So
n(B)=6
P(B)=n(B)/n(S) =6/16=⅜

📌 Ex15. A fair coin is tossed 30 times, the result of which is tabulated below study the table and answer the questions given below the table:

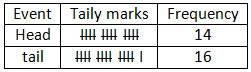
(i). How many times does ‘head’ appear?
Ans: Appearance of ‘head’ in experiment are 14.
(ii). How many times does ‘tail’ appear?
Ans: Appearance of ‘tail’ in experiment are 16 times.
(iii). Estimate the probability of the appearance of head?
Ans: n(H)=14;n(S)=30
P(H)=n(H)/n(S)=14/30=7/15
(iv) Estimate the probability of the appearance of tail?
Ans: n(T)=16;n(S)=30
P(T)=n(T)/n(S)=16/30=8/15

📌 Ex16. A fair coin is tossed four times, and a person win cent 1 for each head and lose cent 1.50 for each tail that turns up.
From the sample space calculate how many different amounts of money you can have after four tosses and the probability of having each of these amounts.
✍ Solution:
Since the coin is tossed four times, there can be a maximum of 4 heads or tails.
When 4 heads turns up, cent 1 + cent I + cent 1 + cent 1 = cent 4 is the gain.
When 3 heads and 1 tail turn up, cent 1 + cent 1 + cent 1 – cent 1.50 = cent 3 – cent 1.50 = cent 1.50 is the gain.
When 2 heads and 2 tails turns up, cent 1 + cent 1 – cent 1.50 – cent 1.50 = – cent 1, i.e., cent 1 is the loss.
When 1 head and 3 tails turn up, cent 1 – cent 1.50 – cent 1.50 – cent 1.50 = – cent 3.50, i.e., cent 3.50 is the loss.
When 4 tails turn up, – cent 1.50 – cent 1.50 – cent 1.50 – cent 1.50 = – cent 6.00, i.e., cent 6.00 is the loss.
There are 2^4=16 elements in the sample space S, which is given by:
S={HHHH,HHHT,HHTH,HTHH,THHH,HHTT,HUH,TTHH,HTHT,THTH,THHT,HUT,THTT,UHT,TTTH,TTTT}
∴ n(S)=16
The person wins cent 4.00 when 4 heads turn up, i.e., when the event {HHHH} occurs.
∴ Probability (of winning cent 4.00) =1/16
The person wins cent 1.50 when 3 heads and one tail turn up, i.e., when the event {HHHT,HHTH,HTHH,THHH} occurs.
∴ Probability (of winning cent 1.50) =4/16=¼
The person loses cent 1.00 when 2 heads and 2 tails turn up, i.e., when the event
{HHTT,HUH,TTHH,HTHT,THTH,THHT} occurs.
∴ Probability (of losing cent 1.00) =6/16=⅜
The person loses cent 3.50 when 1 head and 3 tails turn up, i.e., when the event {HTTT,THTT,TTHT,TTTH} occurs.
∴ Probability (of losing cent 3.50) =4/16=¼
The person loses Rs 6.00 when 4 tails turn up, i.e., when the event {TTTT} occurs.
∴ Probability (of losing cent 6.00) =1/16