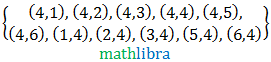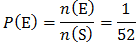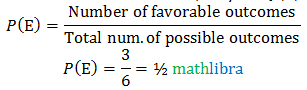Example 1.
In a musical chairs game, a person has been advised to stop playing the music at any time within 40 seconds after its start. What is the probability that the music will stop within the first 15 seconds?
solution:
Total result =0 sec to 40 sec
Total possible outcomes =40→n(S)=40
Favorable results =0 sec to 15 sec
Favorable outcomes =15→n(E)=15
Probability that the music will stop in first 15 sec

Example 2.
In a musical chair game, the person playing the music has been advised to stop playing the music at any time within 2 minutes after she starts playing. What is the probability that the music will stop within the first half-minute after starting?
solution: Here the possible outcomes are all the numbers between 0 and 2. This is the portion of the number line from 0 to 2 (see the given picture).

Let E be the event that ‘the music is stopped within the first half-minute’.
The outcomes favorable to E are points on the number line from 0 to ½.
The distance from 0 to 2 is 2, while the distance from 0 to ½ is ½.
Since all the outcomes are equally likely, we can argue that, of the total distance of 2, the distance favorable to the event E is ½.

Can we now extend the idea of Example 2 for finding the probability as the ratio of the favorable area to the total area?

If n(S) and n(E) are both infinite, the probability can
be estimated by geometrical method as below:

respectively as the sample points (outcomes) are distributed over a length (one dimensional) or an area (two dimensional) or a volume (three dimensional)

Ex3. A hockey match is played from 4 PM to 6 PM. A boy arrives to see the match (not before the match starts). What is the probability that he will miss the only goal of the match which takes place at the 15th minute of the match?
solution:
To arrive at the match the by has to reach between 4 PM to 6 PM. So, the total possible length of time =2 hours =120 minutes.
He will miss the goal if he arrives between 4.15 PM and 6 PM. So, the favourable length of time =1 hour 45 minutes =105 minutes.
Hence the required probability
=105/120=⅞

Ex4. A missing helicopter is reported to have crashed somewhere in therectangular region shown in this figure.

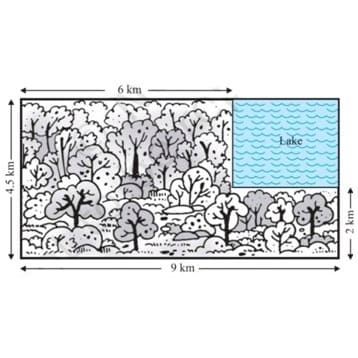
What is the probability that it crashed inside the lake shown in the figure?
solution: The helicopter is equally likely to crash anywhere in the region.
Area of the entire region where the helicopter can crash
=(4.5×9) km²=40.5km²Area of the lake =(2.5×3) km²=7.5 km²
Therefore. P(heliconter crashed in the lake)=7.5/40.5=75/405=5/27

Ex5. Suppose you drop a die at random on the rectangular region shown in the given figure. What is the probability that it will land inside the circle with diameter 1 m?

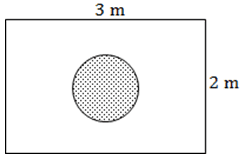
solution:
Area of rectangle =3 m×2 m=6 m². Area of circle (of diameter 1 m)
=πr²=π(½)²=¼πm²
P(die will land inside the circle)=(¼π)/6=π/24

Ex6. A circle with diameter 20 cm is drawn somewhere on a rectangular piece of paper with length 40 cm and width 30 cm. This paper is kept horizontal on table top and a die, very small in size, is dropped on the rectangular paper without seeing towards it. If the die falls and lands on paper only, find the probability that it will fall and land:
(i) inside the circle (ii) outside the circle
solution:
Diameter of the circle =20 cm
Radius =10 cm
Area of circle πr²=22/7×10×10= 2200/7 cm²
Length of paper =40 cm
Width of paper =30 cm
Area of paper =1200 cm²
Total possible outcomes =area of rectangular paper
(i) Since paper is kept on table top and die falls and lands on paper.
Number of favorable outcomes =area of circle. If these
P(C)=P(inside the circle), a(C)=a(area of circle), a(R)=a(area of rectangular paper) then

(ii) P(outside the circle) =1-P(inside the circle)

Ex7. The surface of a soccer ball is made up of 32 faces. 12 faces are regular pentagons, each with a surface area of about 37 cm². The other 20 faces are regular hexagons, each with a surface area of about 56 cm².
You roll the soccer ball. What is the probability that it stops with a pentagon touching the ground?
solution:
Since a soccer ball is round, the probability of stopping on a face is proportional to the area of the face. There are 12 pentagons each with an area of 37 cm², for a total area of 12×37=444 cm². There are 20 hexagons each with an area of 56 cm², for a total area of 20×56=1120 cm². So the probability of stopping on a pentagon is

to 2 decimal places.

Ex8. There is a rectangle of 4 cm by 5 cm. One point is selected at random. What is the probability that minimum distance of this point from any of the four sides of the rectangle is less than 1 cm?
a. 0.3 b. 0.5 c. 0.7 d. 0.8
correct: c, solution:
The point can be 1 cm away from all the four sides. Hence the difference of the area of onginal box and area of the box formed by reducing the sides by 2 cm i.e (3×2) is the area where the point can be placed. The probablity =

Ex9. If a thread is cut off from a point, then what is the probability that the larger part is at least three times the smaller one?
a. ⅓ b. ½ c. ⅔ d. ¼
correct: b, solution:
If the thread is cut off, the cutting off can lie in an of the four regions ranging from 0 to ¼th, ¼th to ½, ½ to ¾th or ¾ to 1.

Now the length of the greater part will be always more than 3 times the smaller part, if the cut is in the 1st or 4th part. Hence Probability =½.