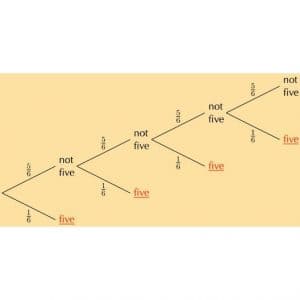
Ex1. A bag contains 3 white, 5 black and 2 red balls, all of the same shape and size. A ball is drawn from the bag without looking into it, find the probability (P) that the ball drawn is:
(i) a black ball.
(ii) a red ball.
(iii) a white ball.
(iv) not a red ball.
(v) not a black ball.
solutions:
Total number of balls =3+5+2=10
(i) There are 5 black balls
P(getting a black ball)=5/10=½
(ii) There are 2 red balls
P(getting a red ball)=2/10=⅕
(iii) There are 3 white balls
P(getting a white ball)=3/10
(iv) There are 3+5=8 balls which are not red
P(getting a non red ball)=8/10=⅘
(v) There are 3+2=5 balls which are not black
Favourable number of events =P(A)=5
P(getting a non black ball)=5/10=½

Ex2. A bag contains six identical black balls. A child withdraws one ball from the bag without looking into it. What is the probability that he takes out:
(i) a white ball
(ii) a black ball
solutions:
Possible number of outcomes =6= number of balls in the bag, n(S)=6
(i) E= event of drawing a white ball =number of white balls in the bag =0

n(E)=0
Probability of drawing a white ball
P(E)=n(E)/n(S) =0/6=0
(ii) E= event of drawing a black ball =number of black balls in the bag =6
n(E)=6
Probability of drawing a black ball
P(E)=n(E)/n(S) =6/6=1

Ex3. A bag contains 16 colored balls. Six are green, 7 are red and 3 are white. A ball is chosen, without looking into the bag. Find the probability that the ball chosen is:
(i) red (ii) not red (iii) white (iv) not white (v) green or red (vi) white or green (vii) green or red or white
solutions:
Balls in the bag =16= Number of balls that could be drawn, n(S)=16.
(i) E= Event of drawing a red ball =number of red balls =7, n(E)=7.
Probability of drawing a red ball =n(E)/n(S) =7/16
(ii) Number of not red balls =n(E)=6+3=9.
Probability of drawing a not red ball =n(E)/n(S) =9/16
(iii) E= Event of drawing a white ball =number of white balls =n(E)=3
Probability of drawing a white ball =n(E)/n(S) =3/16
(iv) Number of not white balls =6+7=13
Probability of not drawing a white ball =n(E)/n(S) =13/16
(v) E= Event of drawing a green or a red ball =number of green balls+number of red balls =6+7=13
Probability of drawing a green or a red ball =n(E)/n(S) =13/16
(vi) E= Event of drawing a green or a white ball =number of green balls+number of white balls =6+3=9
Probability of drawing a green or a white ball =n(E)/n(S) =9/16
(vii) E= Event of drawing a green or a white or a red ball =number of green balls+number of white balls+number of red balls. n(E)=16.
Probability of drawing a green or a white or a red ball =n(E)/n(S) =16/16=1, that is the probability of each sure occurrence as each element in the sample space.

Ex4. A ball is drawn at random from a box containing 12 white, 16 red and 20 green balls. Determine the probability that the ball drawn is:
(i) white (ii) red (iii) not green (iv) red or white
solutions:
Total number of balls in the box =48
Total possible outcomes on drawing a ball =48. n(S)=48.
(i) Event of drawing a white ball, n(E)=12
Probability of drawing a white ball =n(E)/n(S) =12/48=¼
(ii) Event of drawing a red ball, n(E)=16
Probability of drawing a red ball =n(E)/n(S) =16/48=⅓
(iii) Event of drawing a green ball, n(E)=20
Probability of drawing a green ball =n(E)/n(S) =20/48=5/12
Probability of not drawing a green ball =1-5/12=7/12
(iv) red or a white ball =12-16=28 balls
Event of drawing a red or white ball, n(E)=28
Probability of not drawing a green ball =n(E)/n(S) =28/48=7/12

Ex5. A bag contains 3 red balls, 4 blue balls and 1 yellow ball, all the balls being identical in shape and size. If a ball is taken out of the bag without looking into it; find the probability that the ball is:
(i) yellow
(ii) red
(iii) not yellow
(iv) neither yellow nor red
solutions:
Total number of balls in the bag =3+4+1=8 balls
Number of possible outcomes =8=n(S)
(i) Event of drawing a yellow ball n(E)=1
Probability of drawing a yellow ball =n(E)/n(S) =⅛
(ii) Event of drawing a red ball n(E)=3
Probability of drawing a red ball =n(E)/n(S) =⅜
(iii) Probability of not drawing a yellow ball =1- Probability of drawing a yellow ball
Probability of not drawing a yellow ball =1-⅛=(8-1)/8=⅞
(iv) Neither yellow ball nor red ball means a blue ball
Event of not drawing a yellow or red ball n(E)=4
Probability of not drawing a yellow or red ball
P=n(E)/n(S) =4/8=½

Ex6. A box contains 7 red balls, 8 green balls and 5 white balls. A ball is drawn at random from the box. Find the probability that the ball is:
(i) white
(ii) neither red nor white. Solution:
solutions:
Total number of balls in the box =7+8+5=20 balls Total possible outcomes n(S)=20
(i) Event of drawing a white ball =E= number of white balls n(E)=5
Probability of drawing a white ball =n(E)/n(S) =5/20=¼
(ii) Neither red ball nor white ball =green ball
Event of not drawing a red or white ball =E= number of green ball n(E)=8
Probability of drawing a white ball =n(E)/n(S) =8/20=⅖

Ex7. A bag contains a certain number of red balls. A ball is drawn. Find the probability that the ball drawn is:
(i) black (ii) red
solutions:
Total possible outcomes =number of red balls.
(i) Number of favorable outcomes for black balls =0
P(black ball)=0
(ii) Number of favorable outcomes for red balls =number of red balls, n(E)=n(S)
P(red ball)=1

Ex8. A bag contains 10 red balls, 16 white balls and 8 green balls. A ball is drawn out of the bag at random. What is the probability that the ball drawn will be:
(i) not red?
(ii) neither red nor green?
(iii) white or green?
solutions:
Total number of possible outcomes =10+16+8=34 balls n(S)=34
(i) Favorable outcomes for not a red ball =favorable outcomes for white or green ball
Number of favorable outcomes for white or green ball =16+8=24=n(E)
Probability for not drawing a red ball =n(E)/n(S) =24/34=12/17
(ii) Favorable outcomes for neither a red nor a green ball =favorable outcomes for white ball
Number of favorable outcomes for white ball =16=n(E)
Probability for not drawing a red or green ball

P=n(E)/n(S) =16/34=8/17
(iii) Number of favorable outcomes for white or green ball =16+8=24=n(E)
Probability for drawing a white or green ball
P=n(E)/n(S) =24/34=12/17

Ex9. An urn contains 10 red and 8 white balls. One ball is drawn at random. Find the probability that the ball drawn is white.
solution:
Total number of possible outcomes n(S)=18 {10 red balls, 8 white balls}
E→ event of drawing white ball
Number of favorable outcomes n(E)=8 {8 white balls}

P=n(E)/n(S) =8/18=4/9

Ex10. A bag contains 3 red balls, 5 black balls and 4 white balls. A ball is drawn at random from the bag. What is the probability that the ball drawn is:
(i) White (ii) Red (iii) Black (iv) Not red
Solutions:
Total number of possible outcomes n(S)=12 {3 red balls, 5 black balls & 4 white balls}
(i) E→ event of getting white ball
Number of favorable outcomes n(E)=4 {4 white balls}
Probability, P=4/12=⅓
(ii) E→ event of getting red ball
Number of favorable outcomes n(E)=3 {3 red balls}

P=n(E)/n(S) =3/12=¼
(iii) E→ event of getting black ball
Number of favorable outcomes =5 {5 black balls}
P(E)=5/12
(iv) E→ event of getting red
Number of favorable outcomes =3 {3 black balls)
P(E)=3/12=¼
Ē→ event of getting a non-red.
P(Ē)=1-P(E)
P(Ē)=1-¼=¾

Ex11. A bag contains 5 white and 7 red balls. One ball is drawn at random. What is the probability that ball drawn is white?
solution:
Total number of possible outcomes =12 {5 white, 7 red}
E→ event of drawing white ball.
Number of favorable outcomes n(S)=5 {white balls are 5}

P(E)=n(E)/n(S) =5/12

Ex12. A bag contains 5 black, 7 red and 3 white balls. A ball is drawn from the bag at random. Find the probability that the ball drawn is:
(i) Red (ii) black or white (iii) not black
Solutions:
Total number of possible outcomes n(S)=5+7+3=15 {5 black, 7 red & 3 white balls}
(i) E→ event of drawing red ball
Number of favorable outcomes n(E)=7 {7 red balls)

P(E)=n(E)/n(S) =7/15
(ii) E→ event of drawing black or white
Number of favorable outcomes n(E)=8 (5 black & 3 white)
P(E)=n(E)/n(S) =8/15
(iii) E→ event of drawing black ball
Number of favorable outcomes n(E)=5 {5 black balls)
P(E)=n(E)/n(S) =5/15=⅓
Ē→ event of not drawing black ball
P(Ē)=1-P(E)
P(Ē)=1-⅓=⅔

Ex13. A bag contains 4 red, 5 black and 6 white balls. A ball is drawn from the bag at random. Find the probability that the ball drawn is:
(i) White (ii) Red (iii) Not black (iv) Red or white
Solutions:
Total number of possible outcomes n(S)=15 {4 red, 5 black, 6 white balls}
(i) E→ event of drawing white ball.
Number of favorable outcomes n(E)=6 {6 white)

P(E)=n(E)/n(S) =6/15=⅖
(ii) E→ event of drawing red ball
Number of favorable outcomes =4 {4 red balls)
P(E)=4/15
(iii) E→ event of drawing black ball
Number of favorable outcomes =5 {5 black balls)
P(E)=5/15=⅓
Ē→ event of not drawing black ball
P(Ē)=1-P(E)
P(Ē)=1-⅓=⅔
(iv) E→ event of drawing red or white ball
Number of favorable outcomes =10 {4 red & 6 white)
P(E)=10/15=⅔

Ex14. A bag contains 3 red balls and 5 black balls. A ball is drawn at random from the bag. What is the probability that the ball drawn is:
(i) Red (ii) Black
Solutions:
Total number of possible outcomes n(S)=8 (3 red, 5 black)
(i) Let E→ event of drawing red ball. n(E)=3

P(E)=n(E)/n(S) =⅛
(ii) Let E→ event of drawing black ball. n(E)=5
P(E)=n(E)/n(S) =⅝

Ex15. A bag contains 5 red, 8 white and 7 black balls. A ball is drawn at random from the bag. Find the probability that the drawn ball is
(i) red or white (ii) not black (iii) neither white nor black.
Solutions:
Total number of possible outcomes n(S)=5+8+7=20 (5 red, 8 white & 7 black)
(i) E→ event of drawing red or white ball
Number of favorable outcomes n(E)=13 {5 red, 8 white)

P(E)=n(E)/n(S) =13/20=0.65
(ii) getting a non-black ball means getting a red ball or a white one.
P=13/20=0.65
(iii) Let E→ be event of getting neither white nor black ball. That means getting a red ball, n(E)=5
P(E)=n(E)/n(S) =5/20=¼

Ex16. A bag contains 8 red, 6 white and 4 black balls. A ball is drawn at random from the hail.
Find the probability that the drawn ball is
(i) Red or white (ii) Not black (iii) Neither white nor black
Solutions:
Total number of possible outcomes n(S)=8+6+4=18 (8 red, 6 white, 4 black)
(i) Probability of getting a red or a white ball

P=(8+6)/18=7/9
(ii) getting a not black ball means getting a red or a white ball. The probability is
P=(8+6)/18=7/9
(iii) getting neither white nor black means getting a red ball. The probability is
P=8/18=4/9

Ex17. There are 5 green and 3 red balls in a box, one ball is taken out. find the probability in each case:
Events Happening:
(i). The ball is green
Solution:
Total number of balls =n(S)=5+3=8
One ball is taken as random.
Let event A denote that the ball is green. So, total possible outcomes = 8. Favorable outcomes =n(A)=5.

P(A)=n(A)/n(S) =⅝
(ii) The ball is red
Solution:
Total number of balls =n(S)=5+3=8. One ball is taken as random. Let event B denote that the ball is red. So, total possible. Outcomes = 8. Favorable outcomes =n(A)=3
P(B)=n(B)/n(S) =⅜

Ex18. A bag contains 40 balls out of 5 are green, 15 are black and the remaining are yellow. A ball is taken out of the bag. Find the probability in each case:
Event Happening:
(i). The ball is black
Solution:
Total balls n(S)=40
Green balls =5
Black balls =15
Yellow balls =40-20=20
Let event A denote that the ball is black.
Favourable outcomes =n(A)=15

P(A)=n(A)/n(S) =15/40=⅜
(ii). The ball is green
Solution:
Let event B denote that the ball is green.
Favourable outcomes =n(B)=5
P(B)=n(B)/n(S) =5/40=⅛
(iii). The ball is not green
Solution:
Let event C denote that the ball is not green.
P(C)=1-P(ball is green)=1-P(B)
=1-⅛=⅞

Algebraic inserts

Ex19. A bag contains 5 red balls and some blue balls. If the probability of drawing a blue ball is double that of a red ball, determine the number of blue balls in the bag.
solution:
Let the number of blue balls be x.
Number of red balls =5
Total number of balls =x+5

Hence, number of blue balls =10

Ex20. A box contains some black balls and 30 white balls. If the probability of drawing a black ball is two-fifths of a white ball; find the number of black balls in the box.
solutions:
Let the number of black balls in the box be x. Total number of balls in the box =x+30

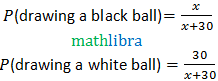
But, P(drawing a black ball)=⅖×P(drawing a white ball)

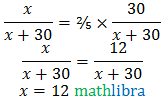
Number of black balls in the box =12

Ex21. A box contains 12 balls out of which x are black. If one ball is drawn at random from the box, what is the probability that it will be a black ball? If 6 more black balls are put in the box, the probability of drawing a black ball is now double of what it was before. Find x.
solution:
Total number of balls =12
Total number of black balls =x
P(getting a black ball)=x/12
If 6 more black balls are put in the box, then
Total number of balls =12+6=18
Total number of black balls =x+6
P(getting a black ball now)=(x+6)/18
According to the condition given in the question,
Total number of black balls =x
P(getting a black ball)=x/12
If 6 more black balls are put in the box, then
Total number of balls =12+6=18
Total number of black balls =x+6
P(getting a black ball now)=(x+6)/18
According to the condition given in the question,

Ex22. A bag contains 6 red balls and some blue balls. If the probability of drawing a blue ball the bag is twice that of a red ball, find the number of blue balls in the bag.
solution:
Number of red balls =6
Let number of blue balls =x
Total number of possible outcomes =6+x (total number of balls)

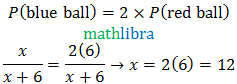
Number of blue balls =12