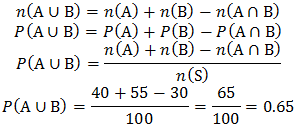Mutually Exclusive Events
Two events is called mutually exclusive if the two events can not occur at the same time (simultaneously). Two eventswhich are mutually exclusive do not have intersection sample points or do not have A∩B=∅. If two events have intersection sample points then the two events are called not mutually exclusive. Event A and B are not mutually exclusive if A∩B≠∅.

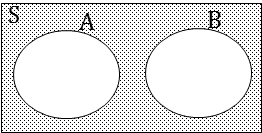
A and B are mutually exclusive

A and B are not mutually exclusive
Probability of the union of two event which are mutually exclusive
In experiment of a die throwing, suppose A is the event of the emerging of die eyes is 4, P(A)=⅙. Suppose B is the emerging of die eyes is 2, P(B)=⅙. Event A and event B are mutually exclusive. Probability of getting 4 on dice A or 2 on dice B, we can write as P(A∪B), and P(A∪B)=2/6. Note that P(A)+P(B)=P(A∪B).

If events A and B are mutually exclusive then probability of event A or B which are occured is:
P(A∪B)=P(A)+P(B)
If events A and B are not mutually exclusive then probability of event A or B which are occured is:
P(A∪B)=P(A)+P(B)-P(A∩B)

Example 2: In the tossing of the 2 balance dice simultaneously, determine the probability:
a. The emerging of the sum of dice eyes equals 8 or 10
b. The emerging of the sum of dice eyes shows prime number or even one.
The explanation:
Sample space of the sum of dice eyes from the tossing of two balance dice are as the following table:

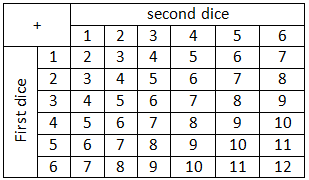
The amount of members of the sample space = 36.
a. Suppose A is the event of emerging of the sum of dice eyes are equal to 8 then P(A)=5/36. Suppose B is the event of emerging of the sum of dice eyes are equal to 10 then P(B)=3/36. Probability of events of the emerging of the sum of dice eyes are equal to 8 or 10 is:

P(A∪B)=P(A)+P(B)=5/36+3/36=8/36
b. Suppose X is the event of the emerging of the sum of dice eyes is prime number then:

X={2,3,5,7,11} and P(X)=15/36
Suppose Y is the event of the emerging of the sum of dice eyes is even number then:

Y={2,4,6,8,10,12} and P(X)=18/36
Since X and Y have the intersection of sample points which is 2 then X and Y are not mutually exclusive, and n(X∩Y)=1.

P(X∪Y)=P(X)+P(Y)-P(X∩Y)
=15/36+18/36-1/36=32/36Exercise Competency Test 2 of Probability part III
Instruction: Choose the one correct answer.
1. Let there are 12 cards which are numbered from 1 to 12. If one card is withdrawn at random then the probability of prime or odd numbered card is …
A. 11/12 B. 10/12 C. 9/12 D. 8/12 E. 7/12
Correct: E the explanation:
Method I: Use P(A∪B)=P(A)+P(B)-P(A∩B)
Suppose A denote the elements of prime numerals are

{2,3,5,7,11}→n(A)=5
Suppose B denote the elements of odd numerals are

{1,3,5,7,9,11}→n(B)=6
A and B have same elements {3,5,7,11}→n(A∩B)=4
Thus the elements of A and B are {1,2,3,5,7,9,11}

n(A∪B)=7
I wanna just show you this proven

n(A∪B)=n(A)+n(B)-n(A∩B)
7=5+6-4
P(A∪B)=P(A)+P(B)-P(A∩B)
P(A∪B)=5/12+6/12-4/12
P=7/12
Method II: Registering elements.
the elements of prime or odd numerals are {1,2,3,5,7,9,11}

P=7/122. A bag contains 5 red balls, 3 white ones and 2 green ones. A ball is taken, the probability of red ball or green one taken is …
A. ⅘ B. 7/10 C. ⅓ D. ½ E. 1/10
correct: B, the explanation:
Suppose A shows a red ball taken, n(A)=₅C₁=5
Suppose B shows zero white ball taken, n(B)=0
Suppose C shows a green ball taken, n(BC)=₂C₁=2
A, B and C are mutually exclusive.

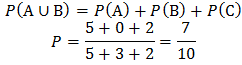
3. Two balance dice are thrown at the same time. Probability of the emerging of the sum of dice eyes equals 3 or 10 is …
A. 5/36 B. ⅙ C. 7/36 D. 2/9 E. ¼
correct: C, the explanation:
A die has 6 side. The sample space of two dice equals 6×6=36. Look at the table on example 2 above. The number of sum equal 3 or 10 is 7.

P=(4+3)/36=7/364. From 100 students who are registered, 40 people attend statistics course, 55 people attend calculus course and 30 attend the two course. If one of the 100 students is called, then probability of the student which is called attends statistics course or calculus course is equal to …
A. 0.95 B. 0.85 C. 0.75 D. 0.65 E. 0.55
correct: D, the explanation:
Suppose n(A) denote the number of students attending statistics.
Suppose n(B) denote the number of students attending calculus.
Suppose n(A∩B) denote the number of students attending both.
Suppose n(A∪B) denote the number of students attending statistics.
Suppose n(S) is the number of sample space.