Set Subtraction — a Set Operator

Venn Diagrams and Set Subtraction

Sets and relationships between sets are represented visually using Venn Diagrams, which were introduced by mathematician John Venn.

Venn Diagrams
● The universal set 𝕌, which contains all objects under consideration, is represented by a rectangle.
● Circles and other shapes are used inside the rectangle to represent sets (Which are subsets of 𝕌).
● Elements of 𝕌 (or other sets) are represented by dots.

Set Subtraction
Let A and B be any two sets. Subtracting set B from A in this order is the set of all those elements of A which do not belong to B. It is denoted by A–B and read as A minus B. The symbol ‘-’ is used to denote the substraction of set B from A. ∴

A–B={x:x∈A and x∉B}
Similarly,
B–A={x:x∈B and x∉A}
The Set Subtraction between A and B can be represented by the following Venn diagram

Figures (a) Venn Diagram of the set A–B (b) B–A
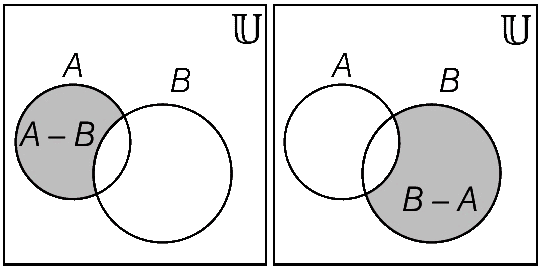
The shaded portion represents the Set Subtraction between A and B.
e.g., Let C={1,2,3,4,5}
and D={3,5,7,9}
Then, C–D={1,2,4}
and D–C={7,9}

⛲ Example 1. E={a,b,d,f},F={b,f,h,i,j}. What is E–F? What is F–E?
🔑 E–F={a,b}. F–E={h,i,j}

Set minus. If A and B are sets, We can create a new set named A–B (spoken as “A minus B”) by starting with the set A and removing all of the objects from A that are also contained in the set B.
Examples.
● {1,7,8}-{7}={1,8}
● {1,2,3,4,5,6,7,8,9,10}-{2,4,6,8,10}={1,3,5,7,9}

⛲ Example 2: The Set Subtraction
Given

𝕌={a,b,c,d,e,f,g,h,i,j,k}
G={b,d,e,f,g,h}
H={a,b,d,h,i}
I={b,e,g}

determine a) G–H b) G–I c) Ḡ-H d) G-Ī
✍ Solution:
a) G–H is the set of elements that are in set G but not set H. The elements that are in set G but not set H are e, f, and g. Therefore. G–H={e,f,g}.
b) G–I is the set of elements that are in set G but not set I. The elements that are in set G but not set I are d, f, and h. Therefore. G–I={d,f,h}.
c) To determine Ḡ-H, we must first detennine Ḡ.

Ḡ={a,c,i,j,k}.
Ḡ-H is the set of elements that are in set Ḡ but not set H. The elements that are in set Ḡ but not set H are c, j, and k. Therefore. Ḡ-H={c,j,k}.
d) To determine G-Ī. we must first determine Ī.
Ī={a,c,d,f,h,i,j,k}.
G-Ī is the set of elements that are in setA but not set Ī. The elements that are in set G but not set Ī are b, e, and g. Therefore, G-Ī={b,e,g}

Next we discuss the Cartesian product.

⛲ Ex3. Let J={1,2,3,4,5,6},K={2,4,6,8}. Find J–K and K–J.
✍ Solution: We have, J–K={1,3,5}, since the elements 1, 3, 5 belong to J but not to K and K–J={8}, since the element 8 belongs to K and not to A. We note that J–K≠K–J.

⛲ Ex4. Let L={a,e,i,o,u} and M={a,i,k,u}. Find L–M and M–L.
✍ Solution: We have, L–M={e,0}, since the elements e, o belong to L but not to M and M–L={k}, since the element k belongs to M but not to L.

We note that L–M≠M–L.

Look figures (a) and (b) above, we conclude some knowledge as below.
[Definition] The subtraction of set T from S is the collection of objects in S that are not in T. The subtraction is written S–T. In curly brace notation