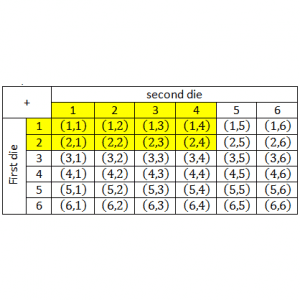
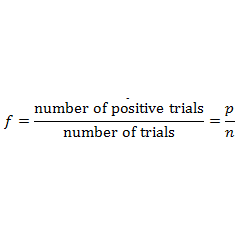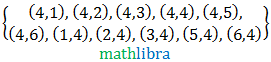There are some symbols you need to use when describing probability. We have used some of them already.
To explain the use of each symbol, we will use these sets again:
S={a; b; c; d; e; f; g; h; i} and A={a; e; i}, B={a; b; c; d; f; g;}, where S= Sample Space, A and B are two sets is the sample space.
| P(A) | means the probability that an element from set A will occur. P(A)=3/9=⅓ |
| n(A) | means the number of elements in set A. n(A)=3 |
| A’ or Ā | means all the elements of the sample space that are NOT in set A. This is the complement of set A. Ā={b,c,d,f,g,h} |
| ∪ | A∪B means the same as A OR B. It means the union of the two sets and represents the total of all the elements that are in set A or set B. No elements are repeated. A∪B={a,b,c,d,e,f,g,i} |
| ∩ | A∩B is the same as A and B. It means the intersection of sets A and B and represents all the elements that they share. (All the elements that are in both set A and set B at the same time). This is where the sets overlap. A∩B={a} |
| P(A∩B) | means the probability that an element from (A∩B) will occur. P(A∩B)=1/9 |
| P(A∪B) | means the probability that an element from (A∪B) will occur. P(A∪B)=8/9 |
| n(A∪B) | means the number of elements in set A or set B. n(A∪B)=8 |
| n(A∩B) | means the number of elements in set A and set B at the same time (the elements they share). n(A∩B)=1 |
| (A∩B)’ | means all the elements of the sample space that are NOT in (A∩B), the complement of (A∩B). (A∩B)={b,c,d,e,f,g,h,i} |
| (A∪B)’ | means all the elements of the sample space that are NOT in (A∪B). (A∪B)’={h} |
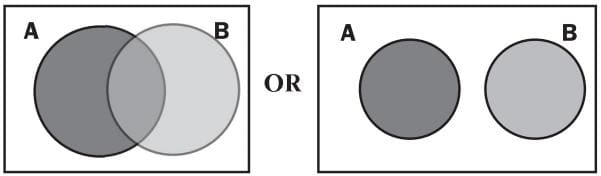
The shaded areas represent:
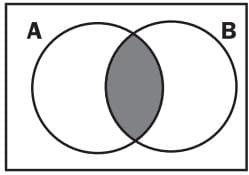
The shaded area represents:
You also need to be able to work with three sets in probability, using a Venn diagram and the formulae.
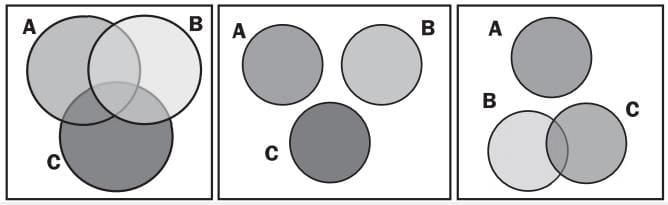
The shaded areas represent:
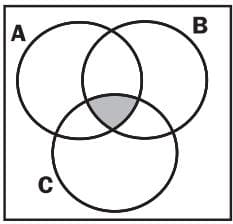
The shaded area represents:

The shaded area represents:
Embed the link of this post