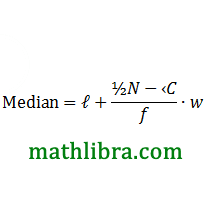The mode (Mo) of a distribution is the value at the point about which the items tend to be most heavily concentrated. It is generally the value of the variable which appears to occur most frequently in the distribution.
1. Mode for a Raw Data
Mode from the following numbers of a variable 70, 80, 90, 96, 70, 96, 96, 90 is 96 as 96 occurs maximum number of times.

Hence, Mo is the maximum frequency.
2. For Grouped Distribution
The class having the maximum frequency is called the modal class and the middle point of the modal class is called the crude mode.
The class just before the modal class is called pre-modal class and the class after the modal class is called the post -modal class.
Mode for Grouped Data (Continuous Distribution)
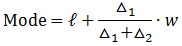
With △1=f–f0;△2=f–f2
Where, ℓ= lower boundary of the modal class
f= frequency of the modal class
f0= frequency of the pre-modal class
f2= frequency of the post-modal class
w= length of the class interval
Mode is value which occurs frequently in a distribution, it a value corresponding to highest frequency. A distribution may be unimodal (single mode) / Bimodal (two modes) / multimodal (many modes).
For discrete frequency distribution and continuous frequency distribution
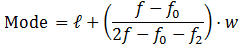
Where,
ℓ: lower boundary of modal class (modal class is the class with highest frequency)
f: frequency of the modal class
f0: frequency preceding to modal class
f2: frequency succeeding to modal class
w: width of modal class
Note 1: To calculate Mode in case of continuous frequency distribution the class intervals should be of Exclusive type.
Note 2: If any one (or more) of the following cases arises then mode is said to be ill defined.
(a) If the maximum frequency is repeated.
(b) If the maximum frequency appears at the very beginning or at the end.
(c) If there are irregularities in the distribution.
Merits:
● It is not affected by extreme values.
● It can be considered as one of the suitable averages in case of a frequency distribution with open end
class intervals.
Demerits:
● It is ill defined.
● It is not based on all observations.
● It is not suitable for further algebraic treatment.
Calculation of Mode
In case of frequency distribution, mode is the value of the variable corresponding to the maximum frequency. In case of continuous frequency distribution, the class corresponding to the maximum frequency is called the modal class and the value of mode is obtained as,

where
ℓ= Lower boundary of modal class
w= Magnitude of the modal class or
w= Size of the model class interval.
f= frequency of the modal class
f0= Frequency of class preceding the modal class
f2= Frequency of class succeeding the modal class
Both f0 and f2 are valid if the classes are in ascending order.
Example 1. Compute the mode of the following
distribution:
Class intervals:
0-6 7-13 14-20 21-27 28-34 35-41 42-48
Frequency:
19 25 36 72 51 43 28
Solution:

Example 2:
| Class Interval | Frequency |
|---|---|
| 6.5 – 7.5 | 5 |
| 7.5 – 8.5 | 12 |
| 8.5 – 9.5 | 25 |
| 9.5 – 10.5 | 48 |
| 10.5 – 11.5 | 32 |
| 11.5 – 12.5 | 6 |
| 12.5 – 13.5 | 1 |
Mode lies in 9.5 – 10.5 class because 48 is the maximum frequency of this class.
We will use formula to determine the mode value, which exists in modal class:

l1= Lower boundary of modal class
l2= Upper boundary of modal class
f= frequency of modal class
f0= frequency of the next lower group than the modal class
f2= frequency of the next higher group than the modal class

• Is the value of the variable that occurs most frequently
• Is the value for which the frequency is maximum
• Example: The number of children in 15 families be as follows
• Mode of the series is 3 because this value occurs most frequently
• Often denoted by Mo & frequently referred to as modal value
• From the frequency distribution the mode can be obtained from the formula

Where,
ℓ= Lower boundary of the modal class (The class containing the mode)
△1= excess of the modal frequency over the class frequencies of the pre modal class
△2= excess of the modal frequency over the class frequencies of the post modal class
w= Size of the modal class interval
Mode
•Mode is the value that has the highest frequency in a data set.
•For grouped data, class mode (or, modal class) is the class with the highest frequency.
•To find mode for grouped data, use the following formula:

Where:
ℓ is the lower boundary of class mode
△1 is the difference between the frequency of class mode and the frequency of the class before the class mode
△2 is the difference between the frequency of class mode and the frequency of the class after the class mode
w is the class width
Example 3: Based on the grouped data below, find the mode.
| Time to travel to work | Frequency |
|---|---|
| 1-10 11-20 21-30 31-40 41-50 |
8 14 12 9 7 |
Solution:
Based on the table,
ℓ=10.5, △1=(14-8)=6, △2=(14-12)=2 and w=10.

Mode can also be obtained from a histogram.
Step 1: Identify the modal class and the bar representing it
Step 2: Draw two cross lines as shown in the diagram.
Step 3: Drop a perpendicular from the intersection of the two lines until it touch the horizontal axis.
Step 4: Read the mode from the horizontal axis

Let’s read post The Quartile Common Formulae for Continuous or Discrete Distribution (Grouped Data).