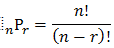Circular Array
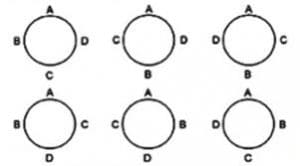
The arranging of elements or objects to be circular is called circular array or circular permutation. Suppose, there are 4 persons sit rounding a circle table, then the circular permutation of that four persons can be drawn as the following.
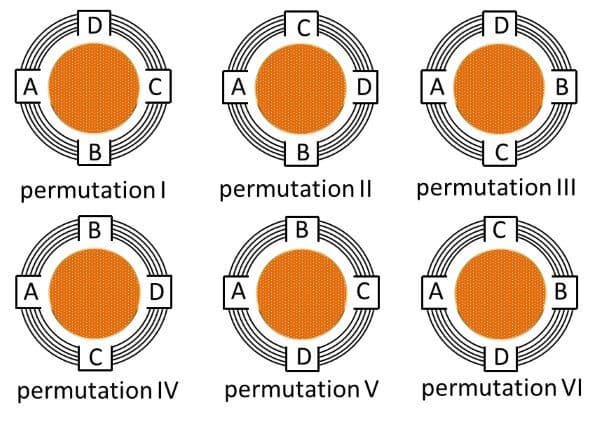
circular permutation
Pay attention that in circular array or circular permutation, shifting or movement of all objects in the rotation does not make anew permutation. Look at the following figure.
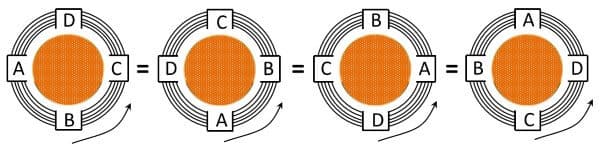
cyclic permutation
By the explanation above, we can conclude that the determining of circular array or circular permutation can be got by deciding an object in one position, the deciding the position possibility of other objects that is left. To determine the number of circular permutation of 4 persons which are surround the circle table, we decide one person to sit at a certain position. Then, the order three will sit as many as 3P3=3!=6 ways. Thus, the number of ways they surround the circle table is equal to 1×6 ways =6 ways.
The number of permutation of n elements which is arranged such circular is equal to (n-1)!
Example 9: The number of permutation if 5 persons are sitting surround a circle table
Exercise Competency Test 9
1. The number of permutation or different array of 6 persons which are sitting surround a circle table =…
A. 720 B. 120 C. 24 D. 12 E. 6
Answer: B, explanation:
2. Ani has 7 pieces of colorful beads which will be arranged to make a bracelet. The number of ways of Ani to arranged yhe beads on the bracelet =…
A. 5040 B. 720 C. 120 D. 24 E. 7
Answer: explanation:

3. Suppose 6 persons will sit surrounding a circle table. If there are two persons which have to sit side by side, then the number of the possible different formation =…
A. 96 B. 48 C. 24 D. 14 E. 12
Answer: B, explanation:
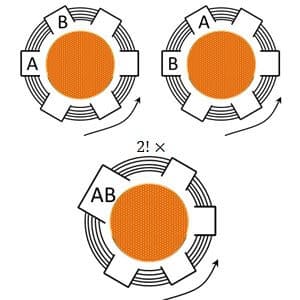
4. Rani will make bracelet which contain of beads. Suppose there are 5 kind of big beads, and 5 kind of small beads. On each bracelet will be filled by 5 kind of big beads and between the big beads there will be 5 small beads. Then, Rani will get some colorful bracelet. The number of bracelet which she can make =…
A. 576 D. 10
B. 36288000 E. 25
C. 597196800000
Answer: A, explanation:
“Between the big beads there will be 5 small beads”.
This sentence means a series “BSBSBSBSBS” only. It is as equivalent as “SBSBSBSBSB” in according to circular array.
=24×24=576
5. Rani has 4 big and 4 small colorful beads, which will be arranged to abracelet. If the small beads have to be between the big beads then the number of ways of Rani to arranged the beads in a bracelet =…
A. 720 B. 144 C. 36 D. 12 E. 7
Answer: explanation:
“The small beads have to be between the big beads”.
This sentence means a series “BSBSBSBS” only. It is as equivalent as “SBSBSBSB” in according to circular array.
=6×6=36