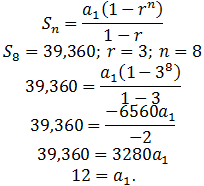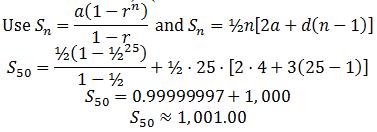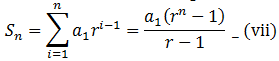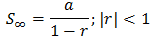A geometric series is the sum of the terms of a geometric sequence.
For example, a geometric sequence is: 6, 12, 24, 48, …
The related geometric series is: 6+12+24+48+…
Sn represents the partial sum of n terms of the series; for example,

The nth term of a geometric series is the nth term of the related geometric sequence.
To derive a rule for determining the sum of the first n terms in any geometric series:
write the sum, multiply each side by the common ratio, r, write the new sum, then subtract vertically.

Divide each side by (1-r) to solve for Sn.

The Sum of n Terms of a Geometric Series
For the geometric series t1+t1⋅r+t1⋅r2+⋯+t1⋅r(n-1), the sum of n terms, Sn, is:
Geometric Series
If the sequence u1, u2, u3, …, un is geometric, then the corresponding series Sn=u1+u2+u3+⋯+un is a geometric series.
The formula for Sn of a geometric series can be written in terms of the first term, a, and the common ratio, r.
If Sn=u1+u2+u3+⋯+un is a geometric series, then:
when |r|>1.
Note: In practice it does not matter which form is used.
To derive this result:

Once we find the first term, a, and the common ratio, r, we can answer any question about a geometric sequence or series.
A geometric series is the sum of the terms of a geometric sequence.
For example:
1, 2, 4, 8, 16, …, 1024 is a finite geometric sequence.
1+2+4+8+16+…+1024 is the corresponding finite geometric series.
If we are adding the first n terms of an infinite geometric sequence, we are then calculating a finite geometric series called the nth partial sum of the corresponding infinite series.
If we are adding all of the terms in a geometric sequence which goes on and on forever, we have an infinite geometric series.
Sum of a Finite Geometric Series
If the first term is u1 and the common ratio is r, then the terms are: u1, u1⋅r, u1⋅r2, u1⋅r3, ….

For a finite geometric series with r≠1.
when |r|>1.

In the case r=1 we have a sequence in which all terms are the same, and Sn=u1⋅n.
Linda starts a chain letter and sends it to three friends. Each of the three friends sends the letter to 3 other friends and the sequence is repeated. Assuming that no one breaks the chain, how many letters will have been sent from the first through the sixth mailings?
Solution: Again, a diagram will help in the understanding of the problem.

On the first mail, 3 letters are sent, on the second mailing there are 3⋅3=9 letters sent, on the third mailing there are 9⋅3=27 letters sent, and so on. So that the sequence formed is 3, 9, 27, … .
The problem asked for the total letters mailed. So the formula for the sum of n terms of a geometric sequence is used.

There are 1092 letters mailed in all.
Example 2: Find the Sum of the First n Terms
In the book Roots, author Alex Haley traced his family history back many generations to the time one of his ancestors was brought to America from Africa. If you could trace your family back for 15 generations, starting with your parents, how many ancestors would there be?
Counting your two parents, four grandparents, eight great-grandparents, and so on gives you a geometric series with a1=2, r=2, and n=15.
Sum formula

Use a calculator.
Going back 15 generations, you have 65,534 ancestors.
Ex3. (Review)
Cora begins a phone tree to notify her friends about a party. In step 1, she calls 3 friends. In step 2, each of those friends calls 3 new friends. In step 3, each of those new friends calls 3 more new friends. After step 3, how many people know about the party, including Cora?
(A) 12 (B) 13 (C) 39 (D) 40
Solution:
First, find the common ratio.
27÷9=3
The common ratio is 3. Find the sum of the series.

Including Cora, 40 people know about the party. Therefore, the correct answer is (D).
Ex4. Use the sequence 128, 64, 32, 16, … 1/512.
Ex4a) How many terms are there?
Okay, it’s geometric, and the common ratio is ½. The general term formula gives un=128⋅½(n-1), and because I know that every number in the list is a power of 2, I’m going to make the formula into just a power of 2. It entertains me.
I can always remember that 25=32 (I don’t know why), and I can see from the list that it takes two more “×2’s” to get me to 128, so 128=27. Also, ½ is 2(-1). So 128⋅½(n-1)=27⋅(2(-1) )(n-1).
The laws of exponents (remember those?) indicate that I should multiply the exponents on the second term, and then add the powers on the twos.
Now 512 is also a power of 2; it’s 29. Just trust me on this. Then 1/512=2(-9). And now 2(8-n)=2(-9), which means 8-n=-9, and n=17. There are 17 terms. I’m coming to the conclusion that I’m working too hard. Counting it out would have worked pretty well.
Ex4b) Find the sum of the terms.

Ex5. A geometric sequence has u6=24 and u11=768. Find the general term of the sequence, and then a couple of other things. First the general term.
For un, I’ll need both the first term and the common ratio. To get from u6 to u1, I get to count! I have to multiply by r… u7, u8, u9, u10, u11… five times. So 24r5=768, which makes it r5=32, and r=2.
To get back from u6 to u1, I’ll have to divide by 2 five times (count it yourself if you don’t believe me). So

And now I have enough for the general term:
un=¾⋅2(n-1).
If you’re feeling all algebraic, you might work out why that’s equivalent to 3⋅2(n-3).
Ex5a) Now we find u17.
Ex5b) And then the sum of the first 15 terms.

Ex6. Find the sum of the first 10 terms of the geometric series 2+1+½+⋯.
Solution: For the series 2+1+½+⋯, a1=2 and r=½=½/1=½.

Ex7. Find the sum of five terms of the geometric series whose first term is 2 and Whose fifth term is 162.
Solution:

Answer: S5=242 or S5=122
Ex8: The sum of a finite geometric series
Find the sum of the series

Solution:
The first term is ⅓, and the common ratio is ⅓. So the nth term can be written as
We can use this formula to find the number of terms in the series:

Because 36=729, we have n=6. (Of course, you could use logarithms to solve for n.) Now use the formula for the sum of six terms of this geometric series:

Ex9. Find the sum of the geometric series
where there are 6 terms in the series.
Solution:
For this series, we have a=2, r=3 and n=6. So

Ex10. Find the sum of the geometric series 8-4+2-1+⋯, where there are 5 terms in the series.
Solution:
For this series, we have a=8, r=-½ and n=5. So

Ex11: Determining the Sum of Given Terms of a Geometric Series
Determine the sum of the first 15 terms of this geometric series:
Write the sum to the nearest hundredth.
solution:
t1= 40 and r is (-20)/40=-½
Use:

Use a calculator.
The sum of the first 15 terms is approximately 26.67.
Ex12: Determining the Sum of a Geometric Series
Calculate the sum of this geometric series:
solution:
t1= 6 and r is 12/6=2
Determine n, the number of terms in the series.
Use: tn=t1⋅r(n-1)
Substitute: tn=12,288, t1=6, r=2
Simplify. Divide each side by 6.
Use guess and test to write 2048 as a power of 2.
Equate exponents.
n=12
There are 12 terms in the series.
Use:

The sum is 24,570.
Ex13. Find the sum of first n terms and the sum of first 5 terms of the geometric series 1+⅔+4/9+⋯
Solution: Here a=1 and r=⅔. Therefore

Ex14: Find each sum.
Ex14a) 24+12+6+3+… to 12 terins Here it’s geometric, with r=½, u1=24, and n=12. The formula:

Ex14b) 1+3+9+… to 5 terms.
Solution:
The given series is a geometric series

Ex14c) 2+6+18+54+⋯ to 12 terms.
solution:
The series is geometric with u1=2, r=3, and n=12.

Ex14d) 25+50+100+… to 6 terms.
Solution:
We need to check if this is an arithmetic series or a geometric series first.
You should see that there is a common ratio of 2 because 50/25=2 and 100/50=2.
∴ It is a geometric series and a=25, n=6, r=2.

So the sum of the first 6 terms of the series is 1, 575.
Ex15. Find the partial sum for the first 20 terms of the series 3+6+12+24+⋯ in the opening example for this section.
Solution:

Ex16: Finding the Sum of a Geometric Series
Find the sum of the first 20 terms of a geometric series if the first term is 1 and r=2.
Let n=20, a1=1, r=2, and use Theorem A.

(Calculation using a calculator)
Ex17: Find the sum of each geometric series described.
Ex17a. first six terms of 3+9+27+⋯
Solution:
First, find the common ratio.
27÷9=3
The common ratio is 3. Use Formula 1 for the sum of a finite geometric series.

Ex17b. first nine terms of 0.5+(-1)+2…
Solution:
First, find the common ratio.
2÷-1 or -2
The common ratio is -2. Use Formula 1 for the sum of a finite geometric series.

Ex17c. first eight terms of 2+2√3+6+⋯
Solution:
First, find the common ratio.
6÷2√3 or √3
The common ratio is √3 . Use Formula 1 for the sum of a finite geometric series.

Ex18. In a geometric ratio the sum of the 4th and 5th terms is 60 and the sum of the 5th and 6th terms is 120. Find the 1st term, the common ratio and the sum of the first 9 terms.
Let the first term be a and the common ratio r, then
a⋅r4+a⋅r5=120 _ (ii).
Factorising and dividing equation (i) by equation (ii).

Substituting for r in equation (i).
24a=60 ∴ a=2½.
Sum of the first 9 terms is given by

Let’s read post Alternate Formula For Sum of Finite Geometric Series — Second Form.