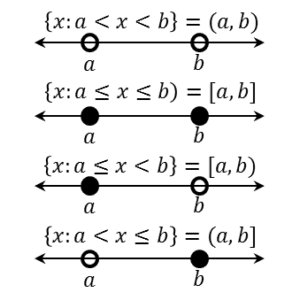Following are some other special sets that you will recall from your study of calculus. Given two numbers a, b∈ℝ with a<b, we can form various intervals on the number line.
• Closed interval: [a,b]={a∈ℝ∶a≤x≤b)}
• Half open interval: (a,b]={a∈ℝ∶a<x≤b)}
• Half open interval: [a,b)={a∈ℝ∶a≤x<b)}
• Open interval: (a,b)={a∈ℝ∶a<x<b)}

On real number line, various types of intervals described above as subsets of ℝ, are shown in the Fig 1.

Fig 1
Here, we note that an interval contains infinitely many points.
For example, the set {x:a∈ℝ,-5<x≤7}, written in set—builder form, can be written in the form of interval as (-5,7] and the interval [-3,5) can be written in set- builder form as {x:-3≤x<5}.

The number (b–a) is called the length of any of the intervals (a,b), [a,b], [a,b) or (a,b].

📌 Example 1. Write the following intervals in set-builder form:
(i) (-3,0)
(ii) [6,12]
(iii) (6,12]
(iv) [-23,5)
🔑
(i) (-3,0)={x∶a∈ℝ, -3<x<0} (ii) [6,12]={x∶a∈ℝ, 6≤x≤12}
(iii) (6,12] ={x∶a∈ℝ, 6<x≤12}
(iv) [-23,5)={x∶a∈ℝ, -23≤x<5} • Infinite interval: (a,∞)={a∈ℝ: a<x}
• Infinite interval: [a,∞)={a∈ℝ∶ a≤x}
• Infinite interval: (-∞,b)={a∈ℝ∶ x<b}
• Infinite interval: (-∞,b]={a∈ℝ∶ x≤b}
Remember that these are intervals on the number line, so they have infinitely many elements. The set (0.1,0.2) contains infinitely many numbers, even though the end points may be close together. It is an unfortunate notational accident that (a,b) can denote both an interval on the line and a point on the plane. The difference is usually clear from context. In the next section we will see still another meaning of (a,b).

Intervals as subsets of ℝ

Let a, b∈ℝ and a<b. Then the set of real numbers {y∶a<y<b} is called an open interval and is denoted by (a,b). All the points between a and b belong to the open interval (a,b) but a, b themselves do not belong to this interval.

The interval which contains the end points also is called closed interval and is denoted by [a,b]. Thus

[a,b]={x:a≤x≤b)}.
We can also have intervals closed at one end and open at the other, i.e.,
[a,b)={x:a≤x<b)} is an open interval from a to b which includes a but excludes b.
(a,b]={x:a<x≤b)} is an open interval from a to b which excludes a but includes b.

These notations provide an alternative way of designating the subsets of set of real numbers. For example,
if A=(-3,5) and B=[-7,9], then A⊂B (read: set A is a prover subset of set B).
(i) (2,8) is a subset of (-1,11).
(ii) [4,6) is a subset of [4,6].
(iii) The set [0,∞) defines the set of non—negative real numbers.
(iv) The set (-∞,0) defines the set of negative real numbers.
(v) (-∞,∞) is the set of real numbers.