General rule of counting
If an event can be occured in n₁ ways, and if that event is followed by other event which can be occured in n₂ ways, if that two events are followed by the third event which can be occured in n₃ ways, …. and so on, the that k continuing events can be occured in (n₁×n₂×n₃×…×n_k) ways.

Example 4:
In how many ways an organization can elect a leader, a secretary and a treasurer from their 10 members?
Answer:
Leader can chosen from the 10 members, means there are 10 ways to elect leader. After we get the leader, the (10-1)=9 members are left to be chosen as secretary, means there are 9 ways to elect secretary.
After we get leader and secretary, then (10-2)=8 members are left to be chosen as the treasurer, means there are 8 ways to chosen the treasurer. So, the ways to elect that three position =(10∙9∙8) ways =720 ways.
Notes: No matter what position which is chosen before the others, the number of ways to chosen is still teh same. Please investigated.
Exercise Competency Test 4
1. There are 4 chairs in a room. If there are 6 persons who will sit in that chairs, then the number of ways for them to sit at the chairs is equal to ….
A. 30 B. 120 C. 360 D. 720 E. 1440
Answer: C, explanation:
Suppose sitting in a series is important for permutation condition. Permutation will be explained so on. One person can not sit on two chairs. One person can sit on a chair only.

2. The numbers which is consist of 3 digits are formed by the numerals: 0, 1, 2, 4. If the numeral used can be repeated, the the amount numbers that can be formed are ….
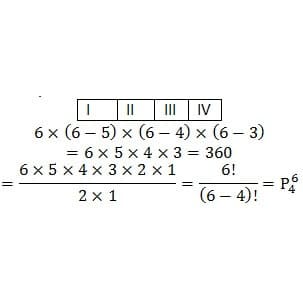
A. 96 B. 64 C. 48 D. 24 E. 12
Answer: C, explanation:
Numeral 0 can not fill room I.

3. Four runners, each of them have ever once at the first position until the last position, until arrive at finish line.
The number of formation (based on position) which can be formed by the 4 runners are ….
A. 256 B. 32 C. 24 D. 16 E. 4
Answer: C, explanation:

=4×(4-1)×(4-2)×(4-3)
=4×3×2×1=24 

4. The numbers which is consist of 3 different numeral with the value is more than three hundred will be formed with the numerals: 1, 2, 3, 4, 5. The amount numbers which are formed is equal to ….
A. 125 B. 75 C. 60 D. 36 E. 24
Answer: D, explanation:
Each of the following numbers is more than three hundred (…>300). It means each numbers starts with {3,4,5}.

5. The numbers which is consist of 3 numeral (numeral used can be repeated) and its value is more than three hundred and will be formed by the numerals: 1, 2, 3, 4, 5. The number of number which are formed is equal to ….
A. 125 B. 75 C. 60 D. 36 E. 24
Answer: A, explanation:

5×5×5=1256. An inn has 6 rooms, they get 4 guests who will stay overnight. The number of ways of the inn employee to place the guests at the rooms =….
A. 360 B. 240 C. 120 D. 24 E. 10
Answer: A, explanation:

=6×(6-1)×(6-2)×(6-2)
=6×5×4×3=360