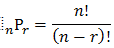Permutation with repetitions
Sometimes in a group of objects provided, there are objects which are alike. If all the objects are arranged, the there will be found the arrangement which are alike or the permutation which are alike. At the preceding example, the number of permutation of letters a, b, c, and d is equal to 24. If the letters a and b are changed by p, while c and d are changed by x, then the letters provided will become p, p, x, and x. Which means they are 2 letters whose are alike of 1st, which is p, and 2 letters whose are alike 2nd, which is x. If these letters are arranged as arranging of a, b, c and d, then we’ll get arrangement as the following:
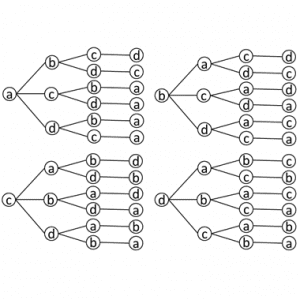
The arrangement of: a, b, c, and d → The arrangement of: p, p, x and x:

abcd→ppxx;abdc→ppxx;acbd→pxpx;acdb→pxxp;adbc→pxpx;
adcb→pxxp;bacd→ppxx;badc→ppxx;bcad→pxpx;bcda→pxxp;
bdac→pxpx;bdca→pxxp;cabd→xppx;cadb→xpxp;cbad→xppx;
cbda→xpxp;cdab→xxpp;cdba→xxpp;dabc→xppx;dacb→xpxp;
dbac→xppx;dbca→xpxp;dcab→xxpp;dcba→xxpp
In the arrangement of letters p, p, x and x, those arrangements are alike, which are:
Ppxx there are 4, pxpx there are 4, pxpx there are 4, xppx there are 4, xpxp there are 4, xxpp there are 4.
Thus the permutation are: ppxx, pxpx, xppx, xpxp and xxpp. The total is 6.
The number of permutation can be formulated by:

The number of permutation or different arrangements of n object of which are n₁ are alike, n₂ are alike, …., and n_k are alike, is equal to:

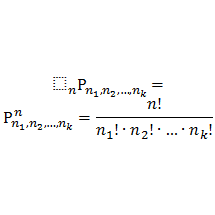
Example 10 (permutation of a word with repeated letters):
Determine the number of permutation of the letters in word MATEMATIKA.
Answer: The number of letters provided=10. There are 2 letters M are alike (1^st type), 3 letters A are alike (2^nd type) , 2 letters T are alike (3^rd type). The number of permutation =

Example Competency Test 10: Permutations with repetitions
1. permutation of a word with repeated letter. The number of different arrangements from the letters in word ADALAH is equal to …
A. 240 B. 120 C. 30 D. 15 E. 6
Answer: B, Explanation:

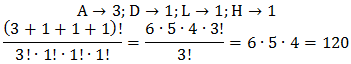
2. The number of permutation from the letters in the word SAMASAJA =…
A. 1680 B. 840 C. 420 D. 210 E. 105
Answer: B, Explanation:

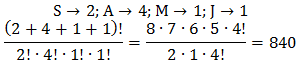
3. Permutation with duplicated element. if 2 same red balls, 3 same yellow balls, and 4 some green balls are arranged in one row, then the number of arrangements is equal to ….
A. 1260 B. 630 C. 315 D. 105 E. 21
Answer: A, Explanation:

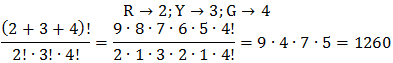
4. Ani will dry underneath the sun 4 white shirts are alike and 6 black pants are alike at a length of rope which is spread out horizontally. The number of possible arrangements is ….
A. 210 B. 105 C. 35 D. 15 E. 10
Answer: A, Explanation:

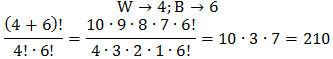
5. Cici has 8 stamps which consist of 5 stamps which is cost 2 cents and 3 stamps is cost 1 cent. If the 8 stamps are stuck in a row, then the number of ways she can do to stick the stamps = …
A. 112 B. 56 C. 28 D. 24 E. 8
Answer: B Explanation: