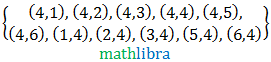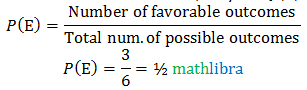Probability of Getting a certain Sum on Rolling or Throwing Two Dice
Ex1. Two dice, one blue and one grey, are thrown at the same time.
(i) Let we calculate respective probabilities of sums being {2,3,4,5,6,7,8,9,10,11,12}.
(ii) A student argues that ‘there are 11 possible outcomes 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 and 12. Therefore, each of them has a probability 1/11. Do you agree with this argument?
Solutions:
Using this table to help calculating each of the probabilities

(ii) Probability of each of these sums will not be 1/11 as these sums are not equally likely.
This example is an exception.
Ex2. A fair coin with 1 marked on one face and 6 on the other and a fair die are both tossed. find the probability that the sum of numbers that turn up is (i) 3 (ii) 12
Solutions:
Since the fair coin has 1 marked on one face and 6 on the other, and the die has six faces that are numbered 1, 2, 3, 4, 5, and 6, the sample space is given by
Accordingly, n(S)=12
(i). Let A be the event in which the sum of numbers that turn up is 3. Accordingly, A={(1,2)}
(ii) Let B be the event in which the sum of numbers that turn up is 12.
Accordingly, B={(6,6)}
Probability of Getting either of Sums on Rolling or Throwing Two Dice
Ex3. A and B throw a pair of dice. If A get a sum 9, find B’s chance of getting a higher sum.
Sol:
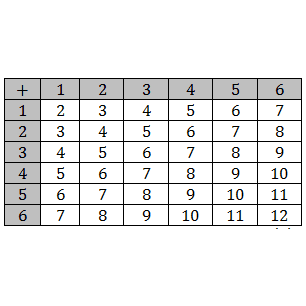
When a pair of dice are thrown, then total number of possible outcomes =6×6=36=n(S), which are shown in this table.
E→ event of throwing a number higher than 9.
Number of favorable outcomes =3+2+1=6=n(E).
The probability is
Ex4. A black die and a white die are thrown at the same time. Write all the possible outcomes. What is the probability?
(i) of obtaining a total more than 9?
(ii) that the sum of the two numbers appearing on the top of the dice is 13?
(iii) that the sum of the numbers appearing on the top of the dice is less than or equal to 12?
Solutions:
Total number of possible outcomes when 2 dice are thrown =6×6=36 which are
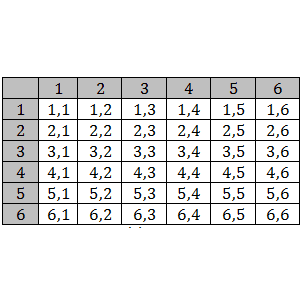
Both pictures are used to solve this question.

(i) E→ event of obtaining a total more than 9
Number of favorable outcomes n(E)=3+2+1=6
(ii) The maximum sum is 12 (6 on 1^st+6 on 2^nd)
So, getting a sum of numbers appearing on the top of the two dice as 13 is an impossible event.
∴ Probability is 0.
(iii) Since, the sum of the numbers appearing on top of 2 dice is always less than or equal to 12, it is a sure event.
Probability of sure event is 1.
So, the required probability is 1.
Ex5. Two dice are rolled, find the probability that the sum is a) equal to 1 b) equal to 4 c) less than 13
Solutions:
a) The sample space S of two dice is shown below.

Let E be the event “sum equal to 1”. There are no outcomes which correspond to a sum equal to 1, hence
b) Three possible ouctcomes give a sum equal to 4: n(E)=3, hence.
c) All possible ouctcomes, E=S , give a sum less than 13, hence.
Ex6. Two dice (each bearing numbers 1 to 6) are rolled together. Find the probability that the sum of the numbers on the upper-most faces of two dice is:
(i) 4 or 5 (ii) 7, 8 or 9 (iii) between 5 and 8
(iv) greater than 10 (v) less than 6
Solutions:
When two dice are rolled, total number of possible outcomes =36

(i) Favorable outcomes for the sums being 4 or 5 are:
Number of favorable outcomes =7
P(getting a sum of 4 or 5) =7/36
(ii) Number of the sums being 7, 8 or 9 is equal to 6+5+4=15.
P(getting a sum of 7.8 or 9) =15/36=5/12
(iii) Favorable outcomes for the sums being between 5 and 8 i.e. 6 or 7. Number of the sums being 6 or 7 is equal to 5+6=11.
P(getting a sum of 6 or 7) =11/36
(iv) Favorable outcomes for the sums being greater than 10 i.e. 11 or 12 are:
Number of favorable outcomes =3
P(getting a sum of numbers greater than 10) =3/36=1/12
(v) Favorable outcomes for the sum of numbers less than 6 I.e. 2, 3, 4 or 5 =10 sums (look at the picture below the question above the (i)). Number of favorable outcomes =10
P(getting a sum of less than 6) =10/36=5/18
Ex7. In a simultaneous throw of a pair of dice, find the probability of getting:
(i) 8 as the sum; (ii) a doublet; (iii) a doublet of prime numbers; (iv) a doublet of odd numbers; (v) a sum greater than 9; (iv) an even number on first; (vii) an even number on one and a multiple of 3 on the other; (viii) neither 9 nor 11 as the sum of the numbers on the faces; (ix) a sum less than 6; (x) a sum less than 7; (xi) a sum more than 7; (xii) at least once; (xiii) a number other than 5 on any dice.
Solutions:
In a throw of pair of dice, total number of possible outcomes n(S)=6×6=36 which are

Both pictures are used to solve the root questions (i) to (xiii).

(i) Let E be event of getting the sum as 8. Number of favorable outcomes n(E)=5.
(ii) E→ event of getting a doublet
Number of favorable outcomes n(E)=6, they are
P(E)=n(E)/n(S) =6/36=⅙
(iii) E→ event of getting a doublet of prime numbers
Number of favorable outcomes n(E)=3, they are
P(E)=n(E)/n(S) =3/36=1/12
(iv) E→ event of getting a doublet of odd numbers
Number of favorable outcomes n(E)=6, they are
P(E)=n(E)/n(S) =3/36=1/12
(v) E→ event of getting a sum greater than 9
Number of favorable outcomes =3+2+1=n(E)=6
(vi) E→ event of getting an even number on first
Number of favorable outcomes is equal to a half of the entire sample space n(E)=½×n(S) as many as odd number on first die rolling.
(vii) E→ event of getting an even number on one and a multiple of 3 on other.
Each even number on a dice {2,4,6} accompanies with each number that multiple of 3 on another die {3,6}, this set will have two pairs (6,6) in. Therefore, call (6,6) once.
Number of favorable outcomes n(E)=(3×2)×2-1=11.
(viii) Ē→ event of getting neither 9 nor 11 as the sum of numbers on faces.
E→ getting either 9 or 11 as the sum of numbers on faces.
Look at the picture below the main question above. Number of favorable outcomes =4+2=6=n(E).
P(Ē)=n(Ē)/n(S) =30/36=⅚
or:
P(E)+P(Ē)=1→P(Ē)=1-P(E)
P(Ē)=1-⅙=⅚
(ix) E→ event of getting a sum less than 6
Look at the picture below the main question above. Number of favorable outcomes =1+2+3+4=10=n(E)
(x) E→ event of getting a sum less than 7
Number of favorable outcomes =1+2+3+4+5=15=n(E)
(xi) E→ event of getting a sum more than 7
Number of favorable outcomes =5+4+3+2+1=15=n(E)
(xii) E→ event of getting a 1 at least once
Number of favorable outcomes n(E)=11, they are
P(E)=n(E)/n(S) =11/36
(xiii) E→ event of getting a pair other than 5 on any dice
Number of favorable outcomes n(E)=(6-1)×(6-1)=25