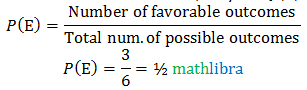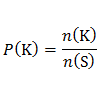In this chapter, you have studied the following points:
1. The difference between experimental probability and theoretical probability.
2. The theoretical (classical) probability of an event E, written as P(E), is defined as
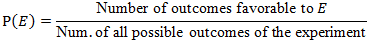
where we assume that the outcomes of the experiment are equally likely.
3. The probability of a sure event (or certain event) is 1.
4. The probability of an impossible event is 0.
5. The probability of an event E is a number P(E) such that
6. An event having only one outcome is called an elementary event. The sum of the probabilities of all the elementary events of an experiment is 1.
7. For any event E, P(E)+P(Ē)=1, where Ē stands for ‘not E’. E and Ē are called complementary events.
A Note To The Reader
The experimental or empirical probability of an event is based on what has actually happened while the theoretical probability of the event attempts to predict what will happen on the basis of certain assumptions. As the number of trials in an experiment, go on increasing we may expect the experimental and theoretical probabilities to be nearly the same.
● An experiment refers to an uncertain process.
● An outcome of an experiment is a single result of that experiment.
● The sample space of an experiment is the set of all possible outcomes of that experiment. The sample space is denoted with the symbol S and the size of the sample space (the total number of possible outcomes) is denoted with n(S).
● An event is a specific set of outcomes of an experiment that you are interested in. An event is denoted with the letter E and the number of outcomes in the event with n(E).
● A probability is a real number between 0 and 1 that describes how likely it is that an event will occur.
◦ A probability of 0 means that an event will never occur.
◦ A probability of 1 means that an event will always occur.
◦ A probability of 0.5 means that an event will occur half the time, or 1 time out of every 2.
● A probability can also be written as a percentage or as a fraction.
● When all of the possible outcomes of an experiment have an equal chance of occurring, we can compute the exact theoretical probability of an event. The probability of an event is the ratio between the number of outcomes in the event set and the number of possible outcomes in the sample space.

● The relative frequency of an event is defined as the number of times that the event occurs during experimental trials, divided by the total number of trials conducted.
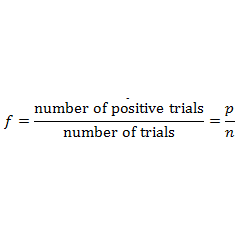
● The union of two sets is a new set that contains all of the elements that are in at least one of the two sets. The union is written as A∪B or “A or B”.
● The intersection of two sets is a new set that contains all of the elements that are in both sets. The intersection is written as A∩B or “A and B”.
● The probability of observing an outcome from the sample space is 1: P(S)=1.
● The probability of the union of two events is calculated using:
● Mutually exclusive events are two events that cannot occur at the same time. Whenever an outcome of an experiment is in the first event, it can not also be in the second event.
● The complement of a set, A, is a different set that contains all of the elements that are not in A. We write the complement of A as Ā or ”not (A)”.
● Complementary events are mutually exclusive: A∩Ā=∅.
● Complementary events cover the sample space: A∪Ā=S
Probabilities of complementary events sum to 1:
Extension: Interpretation of Probability Values
The probability of an event is generally represented as a real number between 0 and 1, inclusive. An impossible event has a probability of exactly 0, and a certain event has a probability of 1, but the converses are not always true: probability 0 events are not always impossible, nor probability 1 events certain. The rather subtle distinction between “certain” and “probability 1” is treated at greater length in the article on “almost surely”.
Most probabilities that occur in practice are numbers between 0 and 1, indicating the event’s position on the continuum between impossibility and certainty. The closer an event’s probability is to 1, the more likely it is to occur.
For example, if two mutually exclusive events are assumed equally probable, such as a flipped or spun coin landing heads-up or tails-up, we can express the probability of each event as “1 in 2”, or, equivalently, “50%” or ” ½”.
Probabilities are equivalently expressed as odds, which is the ratio of the probability of one event to the probability of all other events. The odds of heads—up, for the tossed/spun coin, are (½)/(1-½), which is equal to 1/1. This is expressed as “1 to 1 odds” and often written “1:1”.
Odds a:b for some event are equivalent to probability a/(a+b). For example, 1:1 odds are equivalent to probability ½, and 3∶2 odds are equivalent to probability ⅗.