Number patterns
A list of numbers in order is called a number pattern or number sequence.
We need at least three numbers in the list to work out if the numbers form a pattern. If we only have two numbers, we cannot be sure what the pattern is.
For example, if we have the list 2, 4, … many different number patterns are possible:
The pattern could be 2, 4, 6, …
OR 2, 4, 8, …
OR 2, 4, 2, 4, … add 2 to each number to get the next number
multiply each number by 2 to get the next number
repeat the pattern
A single number in a pattern or sequence is called a term.
Term 1 is written as a₁, term 2 is written as a₂ and so on. The number of the term shows its position in the sequence.
a₁₀ is the 10th term in the sequence. a_n is the nth term in a sequence.

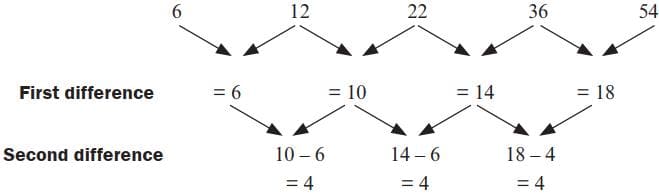
1). Look at the number pattern 3,8,13,…

a₁=3
a₂=8=3+5
a₃=13=8+5
a₄=⋯=13+5
a₅=⋯=⋯+5
If we keep adding 5 to each term we get the next term:

a₄=13+5=18,a₅=23,a₆=28, etc.2). Look at the number pattern 5,15,45,…

a₁=5
a₂=15=5×3
a₃=45=15×3
a₄=⋯=45×3
a₅=⋯=⋯×3
In this pattern, each term is multiplied by 3 to get the next term.
So a₄=45×3+135, a₅=405, a₆=1215, and so on.

3). Look at the sequence: 1,4,9,…

a₁=1², a₂=2², a₃=3²
These are all perfect square numbers. Each number is the number of the term squared. So a₄=4²=16, a₅=5²=25, a₆=6²=36, and so on.

Sequences
Let us consider the following examples:
Assume that there is a generation gap of 30 years, we are asked to find the number of ancestors, i.e., parents, grandparents, great grandparents, etc. that a person might have over 300 years.
The number of person’s ancestors for the first, second, third, tenth generations are 2, 4, 8, 16, 32, …, 1024. These numbers form what we call a sequence.
A sequence containing finite number of terms is called a finite sequence. For example, sequence of ancestors is a finite sequence since it contains 10 terms (a fixed number).
A sequence is called infinite, if it is not a finite sequence. For example, the sequence of successive quotients mentioned above is an infinite sequence, infinite in the sense that it never ends.
Often, it is possible to express the rule, which yields the various terms of a sequence in terms of algebraic formula. Consider for instance, the sequence of even natural numbers 2, 4, 6, ….
Here a₁=2=2×1

a₂=4=2×2
a₃=6=2×3
a₄=8=2×4
⋮
a₂₀=40=2×20
and so on.
In fact, We see that the nth term of this sequence can be written as a_n=2n, where n is a natural number. Similarly, in the sequence of odd natural numbers 1, 3, 5, …, the nth term is given by the formula, a_n=2n-1, where n is a natural number.
In the sequence of primes 2, 3, 5, 7, …, we find that there is no formula for the nth prime. Such sequence can only be described by verbal description.
In every sequence, we should not expect that its terms will necessarily be given by a specific formula. However, we expect a theoretical scheme or a rule for generating the terms a₁, a₂, a₃, …, a_n in succession.
In view of the above, a sequence can be regarded as a function whose domain is the set of natural numbers or some subset of it. Sometimes, we use the functional notation a(n) for a_n.

You must have observed that in nature, many things follow a certain pattern, such as the petals of a sunflower, the holes of a honeycomb, the grains on a maize cob, the spirals on a pineapple and on a pine cone etc.

We now look for some patterns which occur in our day-to-day life. Some such examples are:

(i) Reena applied for a job and got selected. She has been offered a job with a starting monthly salary of $8000, with an annual increment of $500 in her salary. Her salary (in $) for the 1st, 2nd, 3rd, … years will be, respectively

8000, 8500, 9000, ….(ii) The lengths of the rungs of a ladder decrease uniformly by 2 cm from bottom to top (see Fig. A).

 

Fig. A
The bottom rung is 45 cm in length. The lengths (in cm) of the 1st, 2nd, 3rd, …, 8th rung from the bottom to the top are, respectively

45, 43, 41, 39, 37, 35, 33, 31(iii) In a savings scheme, the amount becomes 5/4 times of itself after every 3 years.
The maturity amount (in $) of an investment of $8000 after 3, 6, 9 and 12 years will be, respectively:

10000, 12500, 15625, 19531.25(iv) The number of unit squares in squares with side 1, 2, 3, … units (see Fig. B) are, respectively
1²,2²,3²,….

 

Fig. B
(v) Shakila put $100 into her daughter’s money box when she was one year old and increased the amount by $50 every year. The amounts of money (in $) in the box on the 1st, 2nd, 3rd, 4th, … birthday were

100, 150, 200, 250,…, respectively.In the examples above, we observe some patterns. In some, we find that the succeeding terms are obtained by adding a fixed number, in other by multiplying with a fixed number, in another we find that they are squares of consecutive numbers, and so on.
In this chapter (parent-category), we shall discuss one of these patterns in which succeeding terms are obtained by adding a fixed number to the preceding terms. We shall also see how to find their nth terms and the sum of n consecutive terms, and use this knowledge in solving some daily life problems.

Write the first 4 terms of the sequence. (Assume n begins with 1.)
4) a_n=3n

a₁=3⋅1=3; a₂=3⋅2=6; a₃=3⋅3=9; a₄=3⋅4=12
Answer: 3, 6, 9, 12

5) a_n=3n-5

a₁=3⋅1-5=-2; a₂=3⋅2-5=1; a₃=3⋅3-5=4; a₄=3⋅4-5=7
Answer: -2, 1, 4, 7

6) a_n=3ⁿ

a₁=3¹=3;a₂=3²=9;a₃=3³=27;a₄=3⁴=81
Answer: 3, 9, 27, 81

7) a_n=(-3)ⁿ

a₁=(-3)¹=-3;a₂=(-3)²=9;a₃=(-3)³=-27;a₄=(-3)⁴=81
Answer: -3, 9, -27, 81

8) a_n=(-1)ⁿ

a₁=(-1)¹=1;a₂=(-1)²=1;a₃=(-1)³=-1;a₄=(-1)⁴=1
Answer: -1, 1, -1, 1

9). Write the first five terms of each of the following sequences whose nth term are

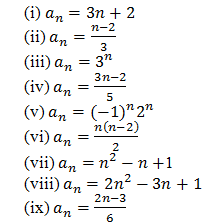
Solution:
We have to write first five terms of given sequences
(i) a_n=3n+2
Given sequence a_n=3n+2
To write first five terms of given sequence, put n=1,2,3,4,5. we get

a₁=(3×1)+2=3+2=5
a₂=(3×2)+2=6+2=8
a₃=(3×3)+2=9+2=11
a₄=(3×4)+2=12+2=14
a₅=(3×5)+2=15+2=17
∴ The required first five terms of given sequence a_n=3n+2 are 5, 8, 11, 14, 17.
(ii)
Given sequence
To write first five terms of given sequence, put n=1, 2, 3, 4, 5 then we get

∴ The required first five terms of given sequence are -⅓, 0, ⅓. ⅔, 1.

(iii) a_n=3ⁿ
Given sequence a_n=3ⁿ
To write first five terms of given sequence, put n=1, 2, 3, 4, 5 in given sequence.
Then,

a₁=3¹=3;a₂=3²=9;a₃=3³=27;a₄=3⁴=81;a₅=3⁵=243.(iv)
Given sequence,
To write first five terms, put n=1,2,3,4,5 in given sequence
Then, we get
∴ The required first five terms are ⅕, ⅘, 1⅖, 2, 2⅗.

(v) a_n=(-1)ⁿ⋅2ⁿ
Given sequence is a_n=(-1)ⁿ⋅2ⁿ
To get first five terms of given sequence, put n=1,2,3,4,5.

a₁=(-1)¹⋅2¹=(-1)⋅2=-2
a₂=(-1)²⋅2²=(-1)⋅4=4
a₃=(-1)³⋅2³=(-1)⋅8=-8
a₄=(-1)⁴⋅2⁴=(-1)⋅16=16
a₅=(-1)⁵⋅2⁵=(-1)⋅32=-32
∴ The first five terms are -2,4,-8,16,-32.

(vi)
The given sequence is,
To write first five terms of given sequence, put n=1,2,3,4,5. Then, we get

The required first five terms are -½, 0, 1½, 4, 7½.

(vii) a_n=n²–n+1
The given sequence is, a_n=n²–n+1
To write first five terms of given sequence, we get put n=1,2,3,4,5. Then we get

a₁=1²-1+1=1
a₂=2²-2+1=3
a₃=3²-3+1=7
a₄=4²-4+1=13
a₅=5²-5+1=21
∴ The required first five terms of given sequence a_n=n²–n+1 are 1,3,7,13,21.

(viii) a_n=2n²-3n+1
The given sequence is a_n=2n²-3n+1
To write first five terms of given sequence, we put n=1,2,3,4,5. Then we get

a₁=2⋅1²-3⋅1+1=2-3+1=0
a₂=2⋅2²-3⋅2+1=8-6+1=3
a₃=2⋅3²-3⋅3+1=18-9+1=10
a₄=2⋅4²-3⋅4+1=32-12+1=21
a₅=2⋅5²-3⋅5+1=50-15+1=36
The required first five terms of given sequence a_n=2n²-3n+1 are 0,3,10,21,36.

(ix)
Given sequence is,
To write first five terms of given sequence, we put n=1,2,3,4,5. Then, we get,

The required first five terms of given sequence a_n=(2n-3)/6 are -⅙,⅙,½,⅚,1⅙.

10). Write the first five terms of the sequences whose nth term is a_n=n(n+2)
Answer:
a_n=n(n+2)
Substituting n=1,2,3,4, and 5, we obtain

a₁=1(1+2)=3
a₂=2(2+2)=8
a₃=3(3+2)=15
a₄=4(4+2)=24
a₅=5(5+2)=35
Therefore, the required terms are 3, 8, 15, 24, and 35.

11). Write the first five terms of the sequences whose nth term is
Answer:
Substituting n=1,2,3,4,5, we obtain

Therefore, the required terms are ½, ⅔, ¾, ⅘ and ⅚.

12). Write the first five terms of the sequences whose nth term is a_n=2ⁿ
Answer:

a_n=2ⁿ
Substituting n=1, 2, 3, 4, 5, we obtain

a₁=2¹=2;a₂=2²=4;a₃=2³=8;a₄=2⁴=16;a₅=2⁵=32.
Therefore, the required terms are 2, 4, 8, 16, and 32.

13). Write the first three terms in each of the following sequences defined by the following:
(i) a_n=2n+5, (ii)
Solution: (i) Here a_n=2n+5. Substituting n=1, 2, 3, we get

a₁=2(1)+5=7,a₂=9,a₃=11.
Therefore, the required terms are 7, 9 and 11.
(ii) Here Thus, a₁=¼(1-3)=-½, a₂=-¼, a₃=0
Hence, the first three terms are -½, -¼ and 0.
Let’s read post How to write the First Few Terms of an Arithmetic Sequence.