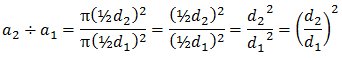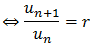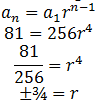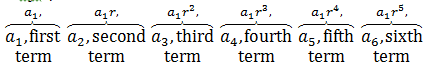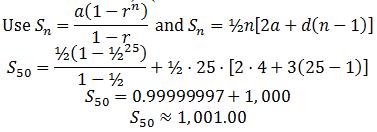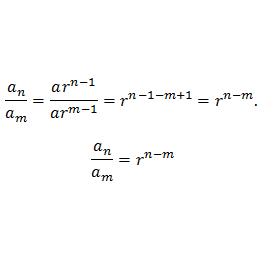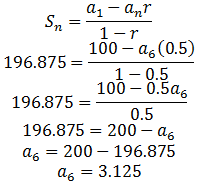Find the common ratio of a Geometric Sequences

The common ratio, r, is found by dividing any term after the first term by the term that directly precedes it. In the following examples, the common ratio is found by dividing the second term by the first term, a₂/a₁ .

Study Tip
When the common ratio of a geometric sequence is negative, the signs of the terms alternate.

Figure A shows a partial graph of the first geometric sequence in our list. The graph forms a set of discrete points lying on the exponential function f(x)=5^(x-1). This illustrates that a geometric sequence with a positive common ratio other than 1 is an exponential function whose domain is the set of positive integers.

How do we write out the terms of a geometric sequence when the first term and the common ratio are known? We multiply the first term by the common ratio to get the second term, multiply the second term by the common ratio to get the third term, and so on.

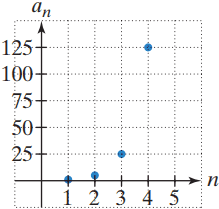
Figure A. The graph of {a_n}=1, 5, 25, 125, …

Geometric Sequence
A sequence a₁, a₂, a₃, …, a_n, …
is called a geometric sequence, or geometric progression, if there exists a nonzero constant r, called the common ratio, such that

That is, a_n=r⋅a_(n-1) for every n>1

A sequence is geometric if each term can be obtained from the previous one by multiplying by the same non-zero constant.
A geometric sequence is also referred to as a geometric progression.

For example:
2, 10, 50, 250, is a geometric sequence as each term can be obtained by multiplying the previous term by 5.
Notice that 10÷2=50÷10=250÷50=5, so each term divided by the previous one gives the same constant.

{u_n} is geometric

for all positive integers n where r is a constant called the common ratio.

For example:
● 2, 10, 50, 250, … is geometric with r=5.
● 2, -10, 50, -250, … is geometric with r=-5.

Geometric sequences
When there is a common ratio (r) between consecutive terms, we can say this is a geometric sequence.

If the first term (a₁) is a, the common ratio is r, and the general term is a_n, then:
r=a₂÷a₁=a₃÷a₂=a_n÷a_(n-1) and a_n=ar^(n-1).

Look at the sequence 5, 15, 45, 135, 405, …
15÷5=3, 45÷15=3 and 135÷45=3 and so the common ratio is 3.
Therefore the sequence is geometric. To get the next term you multiply the preceding term by the common ratio.

Example 1. Find r for the geometric progression whose first three terms are 2, 4, 8.

4÷2=8÷4=2
Then r=2.

Example 2. Find r for the geometric progression whose first three terms are 5, ½, and 1/20.

½÷5=1/20÷½=1/10
Then r=1/10.

A geometric sequence is a sequence of numbers where the ratio of consecutive terms is constant. This ratio is called the common ratio (r). Sometimes the terms of a geometric sequence get so large that you may need to express the terms in scientific notation rounded to the nearest tenth.

2, 6, 18, 54, … This is an increasing geometric sequence with a common ratio of 3.
1, 000, 200, 40, 8, … This is a decreasing geometric sequence with a common ratio or 0.2 or ⅕.

Geometric sequences can also be recursive or explicit. Remember recursive means you need the previous term and the common ratio to get the next term.

Geometric Sequence or Progression (G.P):

A geometric progression is a sequence of numbers each term of which after the first is obtained by multiplying the preceding term by a constant number called the common ratio. Common ratio is denoted by ‘r’.

Example:
This sequence 2, 4, 8, 16, 32, … is G.P because each number is obtained by multiplying the preceding number by 2.

Note:-
In geometric progression, the ratio between any two consecutive terms remains constant and is obtained by dividing the next term with the preceeding term, i.e.,

Example 3. Find the common ratio for the geometric sequence with the given terms.
(a). a₃=12, a₆=187.5
Solution:
The 6th term is 3 terms away from the 3rd term.

187.5=12r³
15.625=r³
2.5=r

(b). a₂=-6, a₇=-192
Solution:
The 7th term is 5 terms away from the 2nd term.

-192=-6r⁵
32=r⁵
2=r

(c). a₄=-28, a₆=-1372
Solution:
The 6th term is 2 terms away from the 4th term.

-1372=-28r²
49=r²
±7=r

(d). a₅=6, a₈=-0.048
Solution:
The 8th term is 3 terms away from the 5th term.

-0.048=6r³
-0.008=r³
-0.2=r

Geometric Sequences and Series

Consider the sequence of numbers 4, 12, 36, 108, … .
Each term, after the first, can be found by multiplying the previous term by 3.
This is an example of a geometric sequence.

A sequence in which each term, after the first, is found by multiplying the previous term by a constant number is called a geometric sequence.

The first term in a geometric sequence is denoted by a.
The constant number, by which each term is multiplied, is called the common ratio and is denoted by r.
Note: r≠-1, 0, 1

Consider the geometric series 3, 6, 12, 24, …
a=3 and r=2
Each term, after the first, is found by multiplying the previous term by 2.
Consider the geometric series 27, 9, 3, 1, …
a=27 and r=⅓
Each term, after the first, is found by multiplying the previous term by ⅓.
Note: Multiplying by 3; is the same as dividing by 3.
In a geometric sequence, the common ratio, r, between any two consecutive terms is always the same.

If three terms, u_n, u_(n+1), u_(n+2) are in geometric sequence, then:

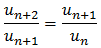
A geometric progression is a list of terms as in an arithmetic progression but in this case the ratio of successive terms is a constant. In other words, each term is a constant times the term that immediately precedes it. Let’s write the terms in a geometric progression as u₁, u₂, u₃, u₄ and so on. An example of a geometric progression is

10, 100, 1000, 10000, …
Since the ratio of successive terms is constant, We have

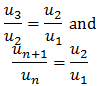
The ratio of successive terms is usually denoted by r and the first term again is usually written a.

Example 4: Geometric sequences
Determine whether the sequence is geometric. If it is geometric, then find the common ratio and the terms a₁, a₃, and a₁₀.

(a) {2ⁿ}

(b) 2, -⅔, 2/9, … , 2(-⅓)^(n-1), …

Solution:

Strategy: The property that identifies a geometric sequence is the common ratio:
the values

must all be the same. For a geometric sequence, use Equatlon (2).

(a) The first few terms are 2, 4, 8, 16, … , each of which is twice the preceding term. This is a geometric sequence with first term a=2, and common ratio given by

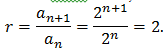
Using a_n=2ⁿ,
a₁=2; a₃=2³=8; a₁₀=2¹⁰=1024.

(b) Consider the ratio

so the sequence is geometric with a=2 and r=-⅓. Using a_n=2(-⅓)^(n-1), we get

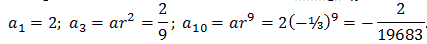
Example 5. In a geometric sequence, the second term is 8 and the fifth term is 64. Find the first term, a, and the common ratio, r. Find the first term, a, and the common ratio, r.
Solution:
(i) u_n=ar^(n-1)
Given: u₂=8. ∴ar=8 … (1)
Given: u₅=64. ∴ar⁴=64 … (2)
We now divide (2) by (1) to eliminate a and find r.

Put r=2 into (1) or (2) to find a:
(1) … ar=8
a⋅2=8
a=4
Thus, the first term is a=4 and the common ratio is r=2.
Note: If the index of r is even, we get two values for r, one positive and the other negative.

Ex6. Find the common ratio of a G.P. of which the third term is 4 and 6th is -32.
Solution:

Here a₃=4, a₆=-32

a_n=ar^(n-1)
a₃=ar^(3-1), a₆=ar^(6-1)
4=ar² … (i); -32=ar⁵ … (ii)
Dividing (ii) by (i)

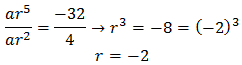
Recall that the product of two negative numbers is positive. So, a square number may be the product of two equal negative numbers or two equal positive numbers. For example,
when r²=4 then r=±2 and r=2 or r=-2.
To determine the common ratio of a geometric sequence, you may need to solve an equation of this form:

r⁴=81
then r²=9
and r=3 or r=-3

Ex7. Three terms in geometric sequence are x-3, x, 3x+4, where x∈R. Find two possible values of x.
Solution:
We use the fact that in a geometric sequence, any term divided by the previous term is always a constant.
Thus, [common ratio]

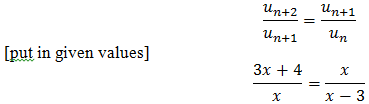
[multiply both sides by (x)(x-3)]
(3x-4)(x-3)=(x)(x)
3x²-5x-12=x²
2x²-5x-12=0
(2x+3)(x-4)=0
2x+3=0 or x-4=0
x=-3/2 or x=4
To verify that a sequence is geometric, we must show the following:

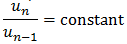
Note: To show that a sequence is not geometric, it is necessary only to show that the ratio of any two consecutive terms is not the same. In practice, this usually involves showing that u₃÷u₂≠u₂÷u₁, or similar.

Ex8. (GEOMETRY) Consider a sequence of circles with diameters that form a geometric sequence: d₁, d₂, d₃, d₄, d₅.

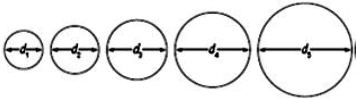
a. Show that the sequence of circumferences of the circles is also geometric. Identify r.
b. Show that the sequence of areas of the circles is also geometric. Identify the common ratio.
Solution:
a. Sample answer: The circumference of a circle is given by C=πd. So, the sequence of circumferences of the circles is πd₁, πd₂, πd₃, πd₄, πd₅.
Find the common ratio.

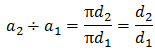
b. Sample answer: The area of a circle is given by A=πr²=π(½d)². So, the sequence of areas of the circles is
π(½d₁)², π(½d₂)², π(½d₃)², π(½d₄)², π(½d₅)².
Find the common ratio.