Geometric sequences
We shall now move on to the other type of sequence we want to explore.
Consider the sequence
2, 6, 18, 54, … .

Here, each term in the sequence is 3 times the previous term. And in the sequence

1, -2, 4, -8, … .
each term is -2 times the previous term. Sequences such as these are called geometric sequences.

Let us write down a general geometric sequence, using algebra. We shall take a to be the first term, as we did with arithmetic sequences. But here, there is no common difference. Instead there is a common ratio, as the ratio of successive terms is always constant. So we shall let r be this common ratio. With this notation, the general geometric sequence can be expressed as

a, ar, ar², ar³, … .
So the n-th can be calculated quite easily. It is ar^(n-1), where the power (n-1) is always one less than the position n of the term in the sequence. In our first example, we had a=2 and r=3, so we could write the first sequence as
2, 2×3, 2×3², 2×3³, … .
In our second example, a=1 and r=-2, so that we could write it as
1, 1×(-2), 1×(-2)², 1×(-2)³, … .

Key Point
A geometric sequence is a sequence where each new term after the first is obtained by multiplying the preceding term by a constant r, called the Common ratio. If the first term of the sequence is a then the geometric sequence is

a, ar, ar², ar³, … .
where the n-th term is ar^(n-1).

Example 1. In a geometric sequence, the fifth term is 80 and the common ratio is -2. Determine the first three terms of the sequence.

a₅=80 and r=-2
a₅=ar⁴=a⋅(-2)⁴=80
16a=80
a=5
∴a₁=5, a₂=5⋅(-2)¹=-10, a₃=5⋅(-2)²=20

Example 2: Creating a Geometric Sequence

Write the sequence in which

a=5, r=3, n=5
answer:
a₁=a=5
a₂=ar=5(3)=15
a₃=a₂ r=15(3)=45
a₄=a₃ r=45(3)=135
a₅=a₄ r=135(3)=405

Therefore, the required sequence is 5, 15, 45, 135, 405.

Write terms of a geometric sequence.
Example 3: Writing the Terms of a Geometric Sequence
Write the first six terms of the geometric sequence with first term 6 and common ratio ⅓.
Solution:
The first term is 6. The second term is 6⋅⅓, or 2. The third term is 2⋅⅓, or ⅔. The fourth term is ⅔⋅⅓, or 2/9, and so on. The first six terms are

6, 2, ⅔, 2/9, 2/27 and 2/81

Use the formula for the general term of a geometric sequence.
The General Term of a Geometric Sequence
Consider a geometric sequence whose first term is a₁ and whose common ratio is r. We are looking for a formula for the general term, a_n. Let’s begin by writing the first six terms. The first term is a₁. The second term is a₁⋅r. The third term is a₁ r⋅r, or a₁⋅r². The fourth term is a₁⋅r²⋅r, or a₁⋅r³, and so on. Starting with a₁ and multiplying each successive term by r, the first six terms are

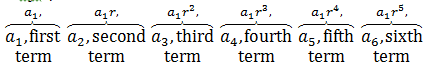
Can you see that the exponent on r is 1 less than the subscript of a denoting the term number?

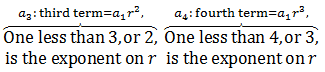
Thus, the formula for the nth term is

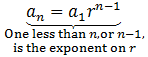
General Term of a Geometric Sequence
The nth term (the general term) of a geometric sequence with first term a₁ and common ratio r is a_n=a₁⋅r^(n-1).

Study Tip
Be careful with the order of operations when evaluating a₁⋅r^(n-1).
First find r^(n-1). Then multiply the result by a₁.

You have seen that each term of a geometric sequence can be expressed in terms of r and its previous term. It is also possible to develop a formula that expresses each term of a geometric sequence in terms of r and the first term a₁. Study the patterns shown in the table on the next page for the sequence 2, 6, 18, 54, … .

The three entries in the last column of the table all describe the nth term of a geometric sequence. This leads us to the following formula for finding the nth term of a geometric sequence.

Key Concept: nth Term of a Geometric Sequence
The nth term a_n of a geometric sequence with first term a₁ and common ratio r is given by

a_n=a₁⋅r^(n-1).
where n is any positive integer.

Example 4: List the first 4 terms of each geometric sequence and find the common ratio (r).
a) a_n=2ⁿ
Solution:

a₁=2¹=2; a₂=2²=4; a₃=2³=8; a₄=2⁴=16
Each term is a multiple of 2 apart so the common ratio is 2.
Answer: First 4 terms 2, 4, 8, 16 common ratio 2
b) a_n=3⋅2ⁿ
Solution:
a₁=3⋅2¹=6; a₂=3⋅2²=12; a₃=3⋅2³=24; a₄=3⋅2⁴=48
Each term is a multiple of 2 apart so the common ratio is 2.
Answer: First 4 terms 6, 12, 24, 48 common ratio 2
c) a_n=½ⁿ
Solution:
a₁=½¹=½; a₂=½²=¼; a₃=½³=⅛; a₄=½⁴=1/16
Each term is a multiple of ½ apart so the common ratio is ½.
Answer: first 4 terms ½, ¼, ⅛, 1/16 and the common ratio is ½.
d) a_n=2³ⁿ
Solution:
a₁=2^(3⋅1)=8; a₂=2^(3⋅2)=64; a₃=2^(3⋅3)=512; a₄=2^(3⋅4)=4096
Each term is a multiple of 8 apart so the common ratio is 8.
Answer: first 4 terms 8, 64, 512, 4096 common ratio 8
e) a_n=2⋅3²ⁿ
Solution:
a₁=2⋅3^(2⋅1)=18; a₂=2⋅3^(2⋅2)=162; a₃=2⋅3^(2⋅3)=1458; a₄=2⋅3^(2⋅4)=13122
Each term is a multiple of 9 apart so the common ratio is 9. Answer: first 4 terms 18, 162, 1458, 13122 common ratio 9.

Example 5: Writing the terms
Write the first five terms of the geometric sequence whose nth term is

a_n=3(-2)^(n-1).
Solution:
Let n take the values 1 through 5 in the formula for the nth term:
a₁=3(-2)^(1-1)=3
a₂=3(-2)^(2-1)=-6
a₃=3(-2)^(3-1)=12
a₄=3(-2)^(4-1)=-24
a₅=3(-2)^(5-1)=48
Notice that a_n=3(-2)^(n-1) gives the general term for a geometric sequence with first term 3 and common ratio -2. Because every term after the first can be obtained by multiplying the previous term by -2, the terms 3, -6, 12, -24, and 48 are correct.

Example 6. Write down the first four terms of the sequence u_n=8⋅¾ⁿ and show that the sequence is geometric.
Solution:

Thus, u_n is a geometric sequence.

Geometric sequences
A geometric sequence has the form
a, ar, ar² ar³, …
in which each term is obtained from the preceding one by multiplying by a constant, called the common ratio and often represented by the symbol r. Note that r can be pos- itive, negative or zero. The terms in a geometric sequence with negative r will oscillate between positive and negative.

The doubling sequence

1, 2, 4, 8, 16, 32, 64, …
is an example of a geometric sequence with first term 1 and common ratio r=2, while
3, -6, 12, -24, 48, -96, …
is an example of a geometric sequence with first term 3 and common ratio r=-2.
It is easy to see that the formula for the nth term of a geometric sequence is
a_n=ar^(n-1).

Definition:
A sequence a₁, a₂, …, a_n, … is called a geometric sequence. If there exists a constant r, such that

a_(k+1)=r⋅a_k; k=1, 2, 3, … .
Thus, a geometric sequence looks as follows:
a, ar, ar², ar³, …
where a is called the first term and r is called as the common ratio of the geometric sequence.
The nth term of the geometric sequence, is given by
a_n=ar^(n-1)
Some other examples of geometric sequences are

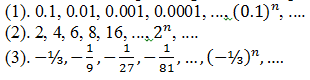
nth term or General term(or, last term) of a Geometric sequence:

If a is the first term and r is the common ratio then the general form of geometric sequence is

a, ar, ar², ar³, … .

If a₁= 1st term =a

a₂= 2nd term =ar
a₃= 3rd term =ar²
…
a_n= nth term =ar^(n-1)
Which is the nth term of geometric sequence in which:
a= first term
r= common ratio
n= number of terms
a_n= nth term=last term

Example 7. Determine the first three terms of a geometric sequence whose 8th term is 9 and whose 10th term is 25.

The first three terms of a geometric sequence is:
9⋅⅗⁷, 9⋅⅗⁶, 9⋅⅗⁵

Example 8. Find a geometric sequence for which sum of the first two terms is -4 and the fifth term is 4 times the third term.
Solution
Let a be the first term and r be the common ratio of the geometric sequence. According to the given conditions,

a₅=4a₃
ar⁴=4ar²
r²=4 ∴r=±2

a₁+a₂=-4
a+ar=-4
a(1+r)=-4
For r=2 then a=(-4)÷(1+2)∴a=-4/3. Also
For r=-2 then a=(-4)÷(1-2)∴a=4.
Thus, the required geometric sequence is -4/3, -8/3, -16/3, … or 4, -8, 16, -32, … .

Example 9: Write down the first four terms with the following situation, will the terms be the first four terms of a geometric sequence?
The amount of air present in the cylinder when a vacuum pump removes each time ¼ of their remaining in the cylinder.
Solution:
Given
Let the initial volume of air in a cylinder be V liters each time ¾ of air in a remaining i.e., (1-¼).
First time, the air in cylinder is V.
Second time, the air in cylinder is ¾V.
Third time, the air in cylinder is ¾² V.
Therefore, the sequence is V, ¾V, ¾² V, ¾³ V, … .
Clearly, this series is a geometric sequence. With first term (a)=V, common ratio (r)=¾.

Example 10. k-1, 2k, and 21-k are consecutive terms of a geometric sequence. Find k.
Solution:
Equating the common ratio r.

Check: If k=7/5 the terms are: ⅖, 7/5, 98/5. ✓ {r=7}

If k=3 the terms are: 2, 6, 18. ✓ {r=3}