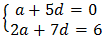If a, b, and c are any consecutive terms of an arithmetic sequence then
b–a=c–b {equating common differences}.
∴2b=a+c
∴b=½(a+c).
So, the middle term is the arithmetic mean of the terms on either side of it.
💎 Arithmetic Mean (A.M):
If a, A, b are three consecutive terms in an Arithmetic sequence, Then A is called the Arithmetic Mean (A.M) of a and b,
i.e. if a, A, b are in A.P. then
A–a=b–A A+A=a+b
2A=a+b A=½(a+b).
The arithmetic mean of two numbers is equal to one half the sum of the two numbers.
If we consider three successive terms in an arithmetic sequence, namely x, y, and z, then since y–x= the common difference, d, and z–y=d, it follows that:
y–x=z–y→y=½(x+z).
The middle term of any three consecutive terms in an arithmetic sequence is called an arithmetic mean and is the average of the outer two terms.
That is, y=½(x+z) for any 3 consecutive terms x, y, z of an arithmetic sequence.
📌 Example 1. Find the A.M. between √5-4 and √5+4
✍ Solution:
Here a=√5-4; b=√5+4.
A.M. =A=½(a+b) A=½(√5-4+√5+4) A=½×2√5=√5
If we need to find three consecutive temis of an arithmetic sequence, we let the numbers be
a–d, a, a+d.
If we need to find five consecutive terms of an arithmetic sequence, we let the numbers be:
a-2d, a–d, a, a+d, a+2d.
Keep ‘a’ in the middle of the sequence.
📌 Ex2. Find k: given that 3k+1, k, and -3 are consecutive terms of an arithmetic sequence.
✍ Solution:
Since the terms are consecutive, k-(3k+1)=-3-k {equating differences},
k-3k-1=-3-k
-2k-1=-3-k
-1+3=-k+2k k=2
or Since the middle term is the arithmetic mean of the terms on either side of it,
k=½[(3k+1)+(-3)]
2k=3k-2 k=2.
📌 Ex3. Three numbers are in arithmetic sequence. Their sum is 24 and their product is 494. Find the three numbers.
✍ Solution:
Let the three terms be (a–d), a, (a+d), which are in arithmetic sequence.
Given: Sum of the three terms =24,
