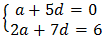💎 Using particular sum formulae as follows:
(i). S_n=½n(a+ℓ)
(ii). S_n=½n(a+a_n)
(iii). S_n=½n(2a+(n-1)d)
(iv). S_n=S_n-1+a_n, i.e., a_n=S_n–S_n-1

📌 Example 1. In an arithmetic sequence, the first term is 2, the last term is 29 and the sum of all the terms is 155. Find the common difference.
✍ Solution:
Here, a=2, ℓ=29 and S_n=155.
Let d be the common difference of the given arithmetic sequence and n be the total number of terms. Then, a_n=29.

a+(n-1)d=29
2+(n-1)d=29 … (i)
The sum of n terms of an arithmetic sequence is given by
S_n=½n(a+ℓ)=155
½n(2+29)=½⋅n⋅31=155
n=10.
Putting the value of n in (i), we get
=2+9d=29
9d=27
d=3.
Thus, the common difference of the given arithmetic sequence is 3.

📌 Ex2. In an arithmetic sequence, the first term is -4, the last term is 29 and the sum of all its terms is 150. Find its common difference.
✍ Solution:
Suppose there are n terms in the arithmetic sequence.
Here, a=-4, ℓ=29 and S_n=150.

S_n=½n(a+ℓ)
½n(-4+29)=150
n=(150⋅2)/25=12.
Thus, the arithmetic sequence contains 12 terms. Let d be the common difference of the arithmetic sequence.
∴ a₁₂=29
[a_n=a+(n-1)d]
-4+(12-1)⋅d=29
11d=29+4=33
d=3.
Hence, the common difference of the arithmetic sequence is 3.

📌 Ex3. The first and last terms of an arithmetic sequence are 5 and 45 respectively. If the sum of all its terms is 400, find the common difference and the number of terms.
✍ Solution:
Suppose there are n term in the arithmetic sequence.
Here, a=5, ℓ=45 and S_n=400.

S_n=400
S_n=½n(a+ℓ)
½n(5+45)=400
n⋅½⋅50=400
n=400÷25
n=16.
Thus, there are 16 terms in the arithmetic sequence. Let d be the common difference of the arithmetic sequence.
∴ a₁₆=45
[a_n=a+(n-1)d]

5+(16-1)⋅d=45
15d=45-5=40
d=40/15=8/3.
Hence, the common difference of the arithmetic sequence is 8/3.

📌 Ex4. In an arithmetic sequence: given a=8, a_n=62, S_n=210, find n and d.
✍ Solution:
Here, a=8, a_n=62 and S_n=210.
The sum of n terms of an arithmetic sequence is given by

S_n=½n(a+a_n)
210=½n⋅(8+62)
210=35n
6=n
⇒a_n=a+(n-1)d
62=8+(6-1)d
54=5d→d=54/5

📌 Ex5. In an arithmetic sequence: given a=3, n=8, S=192, find d.
✍ Solution:
Here, a=3, n=8 and S=192. The sum of n terms of an arithmetic sequence is given by

S_n=½n(a+a_n)
192 =8/2[3+a_n]
192=4[3+a_n]
3+a_n=192/4=48
a_n=45
⇒a_n=a+(n-1)d
45=3+(8-1)d
42=7d
d=6

📌 Ex6. An arithmetic progression has 3 as its first term. Also, the sum of the first 8 terms is twice the sum of the first 5 terms. Find the common difference.
✍ Solution:
We are given that a=3. We are also given some information about the sums S₈ and S₅, and we want to find the common difference. So we shall use the formula

S_n=½n(2a+(n-1)d)
for the sum of the first n terms. This tells us that
S₈=½×8×(6+7d)
and that
S₅=½×5×(6+4d).
So, using the given fact that S₈=2S₅, we see that
½×8×(6+7d)=2×½×5×(6+4d)
4×(6+7d)=5×(6+4d)
24+28d=30+20d
8d=6
d=¾

📌 Ex7. In an arithmetic sequence, the first term is 22, nth terms is -11 and sum of first n terms is 66. Find the number n and the common difference.
✍ Solution:
Here, a=22, a_n=-11 and S_n=66.
Let d be the common difference of the given arithmetic sequence.
Then, a_n=-11

a+(n-1)d=-11
=22+(n-1)d=-11
(n-1)d=-33 … (i)
The sum of n terms of an arithmetic sequence is given by
S_n=½n[2a+(n-1)d]=66
[Substituting the value off (n-1)d from (i)]
½n[2⋅22+(-33)]=½n⋅11=66
n=12.
Putting the value of n in (i), we get:
11d=-33
d=-3.
Thus, n=12 and d=-3.

📌 Ex8. If the sum of first n terms is (3n²+5n), find its common difference.
✍ Solution:
Let S_n denotes the sum of first n terms of the arithmetic sequence.

S_n=3n²+5n
S_n-1=3(n-1)²+5(n-1)
=3(n²-2n+1)+5(n-1)
=3n²–n-2.
Now, nth term of arithmetic sequence, a_n=S_n–S_n-1
=(3n²+5n)-(3n²–n-2)
=6n+2.
Let d be the common difference of the arithmetic sequence.
d=a_n–a_(n-1)
=(6n+2)-[6(n-1)+2]
=6n+2-6(n-1)-2
=6.
Hence, the common difference of the arithmetic sequence is 6.

📌 Ex9. The sum of first n terms of an arithmetic sequence is (3n²+6n). The common difference of the arithmetic sequence is

(a) 6 (b) 9 (c) 15 (d) -3
✍ Solution:
Let S_n denotes the sum of first n terms of the arithmetic sequence.
S_n=3n²+6n
⇒S_n-1=3(n-1)²+6(n-1)
=3(n²-2n+1)+6(n-1)
=3n²-3.
So, nth term of the arithmetic sequence, a_n=S_n–S_n-1=(3n²+6n)-(3n²-3).
=6n+3.
Let d be the common difference of the arithmetic sequence.
∴d=a_n–a_(n-1)=(6n+3)-[6(n-1)+3]
=6n+3-6(n-1)-3
=6.
Thus, the common difference of the arithmetic sequence is 6.
Answer: (a) 6