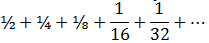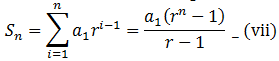We have a=1 and r=½ and so we can calculate some sums. We get
and there seems to be a pattern because
1=2-1
3/2=2-½
7/4=2-¼
15/8=2-⅛
In each case, we subtract a small quantity from 2, and as we take successive sums the quantity gets smaller and smaller. If we were able to add ‘infinitely many‘ terms, then the answer ‘ought to be’ 2– or as near as we want to get to 2.
Let us see if we can explain this by using some algebra. We know that
and we want to examine this formula in the case of our particular example where r=½ Now the formula contains the term rn and, as -1<r<1, this term will get closer and closer to zero as n gets larger and larger. So, if -1<r<1, we can say that the ‘sum to infinity’ of a geometric series is
where we have omitted the term rn. We say that this is the limit of the sums Sn as n ‘tends to infinity‘. You will find more details of this concept in another unit.
👣 Using the formula for the sum of an infinite geometric series.
An infinite sum of the form
a1+a1⋅r+a1⋅r2+a1⋅r3+⋯+a1⋅rn-1+⋯
with first term a1 and common ratio r is called an infinite geometric series. How can we determine which infinite geometric series have sums and which do not? We look at what happens to rn as n gets larger in the formula for the sum of the first n terms of this series, namely
If r is any number between -1 and 1, that is, -1<r<1, the term rn approaches 0 as n gets larger. For example, consider what happens to rn for r=½:
Take another look at the formula for the sum of the first n terms of a geometric sequence.
If -1<r<1, rn ayproaches 0 as n gets larger.
Let us replace rn with 0 in the formula for Sn. This change gives us a formula for the sum of an infinite geometric series with a common ratio between -1 and 1.
🍫 The Sum of an Infinite Geometric Series
If -1<r<1 (equivalently, |r|<1), then the sum of the infinite geometric series
a1+a1⋅r+a1⋅r2+a1⋅r3+⋯
in which a1 is the first term and r is the common ratio, is given by
If |r|≥1, the infinite series does not have a sum.
To use the formula for the sum of an infinite geometric series, we need to know the first term and the common ratio. For example, consider
½+¼+⅛+1/16+1/32+⋯
First term, a1, is ½. Common ratio, r, is a2/a1. r=¼÷½=½.
With r=½, the condition that |r|<1 is met, so the infinite geometric series has a sum given by S∞=a1/(1-r). The sum of the ser1es is found as follows:
Thus, the sum of the infinite geometric series is 1. Notice how this is illustrated in Figure-A. As more terms are included, the sum is approaching the area of one complete circle.
Figur-A. The sum ½+¼+⅛+1/16+1/32+⋯ is approaching 1.
Consider the infinite geometric series ½+¼+⅛+1/16+⋯. You have already learned how to find the sum Sn of the first n terms of a geometric series. For an infinite series, Sn is called a partial sum of the series. The table and graph show some values of Sn.
Notice that as n increases, the partial sums level off and approach a limit of 1. This leveling-off behavior is characteristic of infinite geometric series for which |r|<1.
Study Tip: Absolute Value
Recall that |r|<1 means -1<r<1.
Let’s look at the formula for the sum of a finite geometric series and use it to find a formula for the sum of an infinite geometric series.
Sum of first n terms
Write the fraction as a difference of fractions.
If -1<r<1, the value of rn will approach 0 as n increases. Therefore, the partial
sums of an infinite geometric series will approach
This expression gives the sum of an infinite geometric series. An infinite series that has a sum is called a convergent series.
Key Concept: Sum of an Infinite Geometric Series
The sum S of an infinite geometric series with -1<r<1 is given by
An infinite geometric series for which |r|≥1 does not have a sum. Consider the series 1+3+9+27+81+…. In this series, a1=1 and r=3.
n
Sn
4
121
9
29, 524
14
7, 174, 453
19
1, 743, 392, 200
The table shows some of the partial sums of this series. As n increases, Sn rapidly increases and has no limit. That is, the partial sums do not approach a particular value.
Recall that an infinite series is a series that continues without end. That is, for a series Sn=a1+a2+⋯+an, we say that n approaches infinity. We can also write ∑∞n=1an. However, while there may be an infinite number of terms, a series can behave in only one of four ways. The series may increase without limit, decrease without limit, oscillate, or approach a limit.
CASE 1: The series increases without limit.
Consider an arithmetic series Sn=½n(2a1+(n-1)d). If a1=1 and d=½:
As the Value of n approaches infinity, (n+¼n2) increases without limit. This series has no limit. We can see this by graphing the function Sn=¾n+¼n2 for positive integer Values.
CASE 2: The series decreases without limit.
For an arithmetic series Sn=½n(2a1+(n-1)d). If a1=1 and d=-1:
Sn=½n(2⋅1+(n-1)(-1))
=½n(2-n+1) Sn=½n(3-n)
For this series, as the value of n approaches infinity, ½n(3-n) or (1½n-½n2)decreases without limit. This series also has no limit. We can see this by graphing the function Sn=1½n-½n2 for positive integer values.
CASE 3: The series approaches a limit.
For a geometric series
As n approaches infinity, ½n-1 approaches 0. Therefore, Sn=2-½n-1 approaches Sn=2-0=2 as n approaches infinity. This series has a limit. That diagram shows how the sum of n terms approaches 2 as the number of terms, n, increases.
In general,
► An infinite arithmetic series has no limit.
► An infinite geometric series has no limit when |r|>1.
► An infinite geometric series has a finite limit when |r|<1.
When |r|<1, rn approaches 0. Therefore:
When the ratio of an infinite geometric series is between 0 and 1 or 0 and -1, the sum of the terms is getting closer and closer to a sum.
