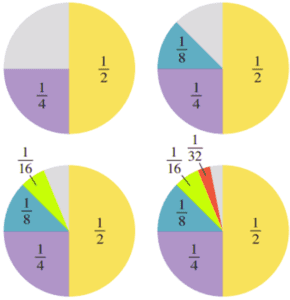
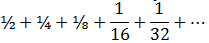In certain cases, the sum of the terms in a geometric sequence has a limit (note that this is summing together an infinite number of terms). A series like this has a limit partly because each successive term we are adding is smaller and smaller (but this fact in itself is not enough to say that the limiting sum exists). When the sum of a geometric series has a limit we say that S_∞ exists and we can find the limit of the sum. The condition that S_∞ exists is that r is greater than -1 but less than 1, i.e. |r|<1. If this is the case, then we can use the formula for S_n above and let n grow arbitrarily big so that rⁿ becomes as close as we like to zero. Then

is the limit of the geometric sequence so long as -1<r<1. 📌 Example 1. The geometric sequence whose first two terms are 2 and 4 doesn’t have S_∞ because r=2≮1.

📌 Ex2. For the geometric sequence whose first two terms are 5 and ½, find S_∞. Note that r=1/10 so |r|<1, so that S_∞ exists. Now

📌 Ex3. For which value(s) of x will 8x²+4x³+2x⁴+⋯ be convergent?
For convergent geometric series, -1<r<1

r=a₂÷a₁
=4x³÷8x²
=½x
-1<r<1 -1<½x<1
Multiply through by 2.
-2<x<2…x≠0
📌 Ex4. Given the series: 3(2x-3)²+3(2x-3)³+3(2x-3)⁴+… for which values of x will the series converge?
✍ Solution:
This is a geometric series with r=2x-3.
To converge -l<r<1 -1<2x-3<1
Add 3 to both sides
2<2x<4 1<x<2,{r≠0, x≠3/2}.
Divide by 2 on both sides.
The series will converge for 1<x<2 📌 Ex5. For which values of x will ∑^∞_k=1 (4x-1)^k exists.
✍ Solution:
r=4x-1
-1<r<1 -1<4x-1<1, x≠¼
0<4x<2 0<x<½

📌 Ex6 ▼
∑^∞_n=0 (2x-3)ⁿ =1+(2x-3)+(2x-3)²+(2x-3)³+⋯ is a geometric series.
(i) Find, in terms of x, the sum to infinity.
(ii) If the sum to infinity is 5/4, find the value of x.
(iii) Find the range of values of x for which the sum to infinity exists.
✍ Solution:
This is an infinite geometric series with first term a=1 and common ratio r=(2x-3).

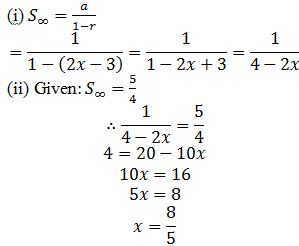
(iii) S_∞ exists if -1<r<1 (i.e. |r|<1) -1<r<1 -1<2x-3<1 (r=2x-3).
Add 3 to each part. 2<2x<4 Divide each part by 2. 1<x<2 Thus, the sum to infinity exists for 1<x<2. 📌 Ex7. (Challenge) For what Values of 19 does 3+9b+27b²+81b³+… have a sum?
✍ Solution:
The common ratio is 9b÷3 or 3b.
The series have a sum, if the absolute Value of the common ratio is less than 1.
That is, |3b|<1. Solve the inequality. |3b|<1 -1<3b<1 -⅓<b<⅓
Therefore, the value of b should be -⅓<b<⅓. Answer: -⅓<b<⅓