When solving a linear programming problem, it is possible that the maximum (or minimum) value occurs at two different vertices. For example, at the vertices of the region shown in Fig-A,

the objective function
z=2x+2y [Objective function]
has the values below.

At (0,0): z=2(0)+2(0)=0 At (0,4): z=2(0)+2(4)=8 At (2,4): z=2(2)+2(4)=12 (Maximum value of z) At (5,1): z=2(5)+2(1)=12 (Maximum value of z) At (5,0): z=2(5)+2(0)=10

In this case, the objective function has a maximum value of 12 not only at the vertices (2, 4) and (5, 1), but at any point on the line segment connecting these two vertices.

Example 1. Minimize and Maximize Z=5x+10y
subject to x+2y≤120, x+y≥60, x-2y≥0, x,y≥0.
✍
The feasible region determined by the constraints, x+2y≤120, x+y≥60, x-2y≥0, x≥0, and y≥0, is as follows.

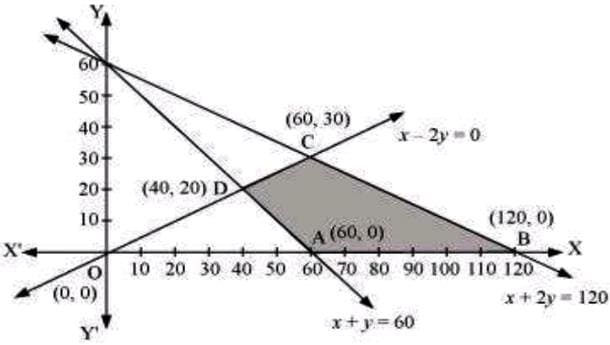
The corner points of the feasible region are A(60, 0), B(120, 0), C(60, 30), and D(40, 20). The values of 2 at these corner points are as follows.

Corner point	Z=5x+10y
A(60,0)	300	→ Minimum
B(120,0)	600	→ Maximum
C(60,30)	600	→ Maximum
D(40,20)	400

The minimum value of Z is 300 at (60, 0) and the maximum value of Z is 600 at all the points on the line segment joining (120, 0) and (60, 30).

Example 2. Minimize and Maximize Z=x+2y
subject to x+2y≥100, 2x–y≤0, 2x+y≤200; x,y≥0.
✍
The feasible region determined by the constraints, x+2y≥100, 2x–y≤0, 2x+y≤200; x≥0, and y≥0, is as follows.

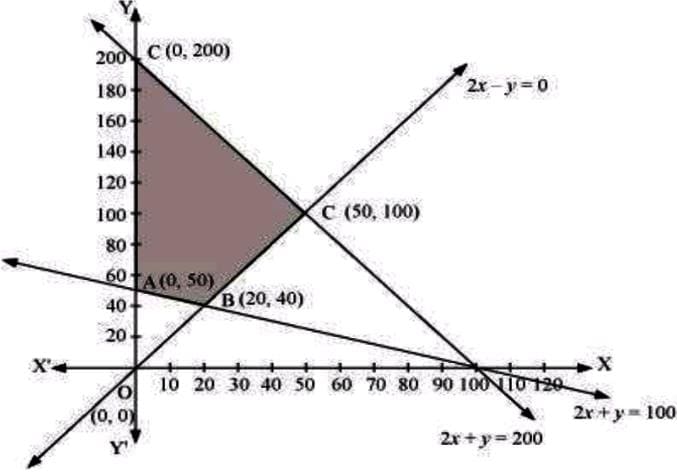
The corner points of the feasible region are A(0, 50), B(20, 40), C(50, 100), and D(0, 200). The values of Z at these corner points are as follows.

Corner point	Z=x+2y
A(0,50)	100	→ Minimum
B(20,40)	100	→ Minimum
C(50,100)	250
D(0,200)	400	→ Maximum

The maximum value of Z is 400 at (0, 200) and the minimum value of Z is 100 at all the points on the line segment joining the points (0, 50) and (20, 40).

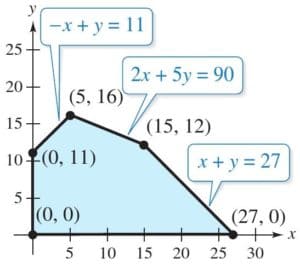
Ex3. Find the maximal and minimal value of z=3x+4y subject to the following constraints:

x+2y≤14, 3x–y≥0, x–y≤2

The three inequalities in the curly braces are the constraints. The area of the plane that they mark off will be the feasibility region. The formula “z=3x+4y” is the optimization equation. I need to find the (x, y) corner points of the feasibility region that return the largest and smallest values of z.
✍
My first step is to solve each inequality for the more-easily graphed equivalent forms:

x+2y≤14, 3x–y≥0, x–y≤2

⇒

y≤-½x+7, y≤3x, y≥x-2

It’s easy to graph the system:

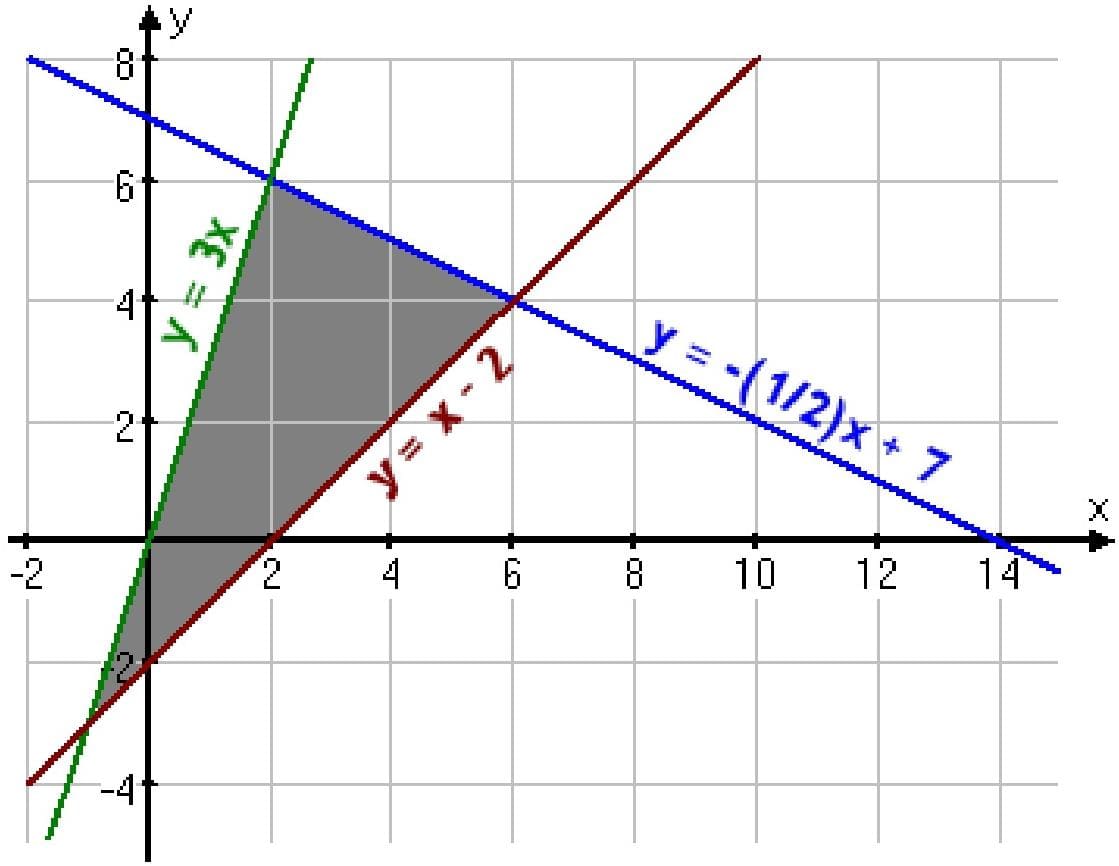
To find the corner points — which aren’t always clear from the graph — I’ll pair the lines (thus forming a system of linear equations) and solve:

y=–½x+7 y=3x	y=–½x+7 y=x–2	y=3x y=x–2
–½x+7=3x –x+14=6x 14=7x 2=x y=3(2)=6	–½x+7=x–2 –x+14=2x-4 18=3x 6=x y=(6)–2=4	3x=x–2 2x=–2 x=–1 y=3(–1)=–3
corner point at (2,6)	corner point at (6,4)	corner pt. at (–1,–3)

So the corner points are (2, 6), (6, 4), and (–1, –3).

Somebody really smart proved that, for linear systems like this, the maximum and minimum values of the optimization equation will always be on the corners of the feasibility region. So, to find the solution to this exercise, I only need to plug these three points into “z=3x+4y”.

(2,6):	z=3(2)+4(6)=6+24=30
(6,4):	z=3(6)+4(4)=18+16=34
(–1,–3):	z=3(-1)+4(-3)=-3-12=-15

Then the maximum of z=34 occurs at (6, 4),
and the minimum of z=–15 occurs at (–1, –3).

Ex4. Solve the following problem graphically:
Minimise and Maximise Z=3x+9y … (1)
subject to the constraints: x+3y≤60 (2)

x+y≥10 … (3)
x≤y … (4)
x≥0,y≥0 … (5)
✍
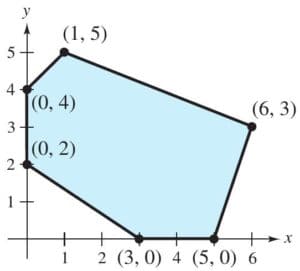
First of all, let us graph the feasible region of the system of linear inequalities (2) to (5). The feasible region ABCD is shown in the Fig-B. Note that the region is bounded. The coordinates of the corner points A, B, C and D are (0, 10), (5, 5), (15, 15) and (0, 20) respectively.

[Fig-B]

Corner Point	Corresponding value of Z=3x+9y
A (0,10) B (5,5) C (15,15) D (0,20)	90 60 ← Minimum 180 ← Maximum 180 ← Maximum

We now find the minimum and maximum value of Z. From the table, we find that the minimum value of Z is 60 at the point B (5, 5) of the feasible region.

The maximum value of Z on the feasible region occurs at the two corner points C (15, 15) and D (0, 20) and it is 180 in each case.

Remark: Observe that in the above example, the problem has multiple optimal solutions at the corner points C and D, i.e. the both points produce same maximum value 180. In such cases, you can see that every point on the line segment CD joining the two corner points C and D also give the same maximum value. Same is also true in the case if the two points produce same minimum value.

Ex5. A fruit grower can use two types of fertilizer in his garden, brand P and brand Q. The amounts (in kg) of nitrogen, phosphoric acid, potash, and chlorine in a bag of each brand are given in the table. Tests indicate that the garden needs at least 240 kg of phosphoric acid at least 270 kg of potash and at most 310 kg of chlorine.
If the grower wants to minimize the amount of nitrogen added to the garden, how many bags of each brand should be used? What is the minimum amount of nitrogen added in the garden?

kg per bag
	Brand P	Brand Q
Nitrogen Phosphoric acid Potash Chlorine	3 1 3 1.5	3.5 2 .5 2

✍
Let the fruit grower use x bags of brand P and y bags of brand Q. The problem can be formulated as follows.
Minimize z=3x+3.5y … (1)
subject to the constraints,

x+2y≥240 … (2)
x+0.5y≥90 … (3)
1.5x+2y≤310 … (4)
x,y≥0 … (5)
The feasible region determined by the system of constraints is as follows.

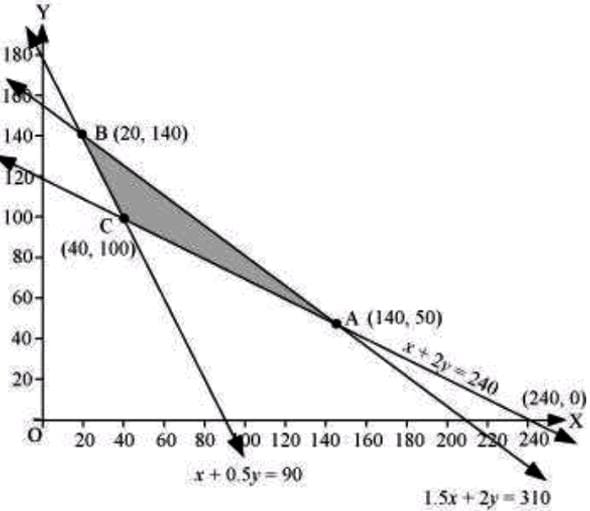
The corner points are A(240, 0), B(140, 50), and C(20, 140). The values of z at these corner points are as follows.

Corner point	z=3x+3.5y
A(140,50)	595
B(20,140)	550
C(40,100)	470	→ Minimum

The minimum value of z is 470 at (40, 100). Thus, 40 bags of brand P and 100 bags of brand Q should be added to the garden to minimize the amount of nitrogen.
The minimum amount of nitrogen added to the garden is 470 kg.

Ex6. Refer to Ex5. If the grower wants to maximize the amount of nitrogen added to the garden, how many bags of each brand should be added? What is the maximum amount of nitrogen added?
✍
Let the fruit grower use x bags of brand P and y bags of brand Q.
The problem can be formulated as follows.
Maximize z=3x+3.5y … (1)
subject to the constraints,

x+2y≥240 … (2)
x+0.5y≥90 … (3)
1.5x+2y≤310 … (4)
x,y≥0 … (5)
The feasible region determined by the system of constraints is as follows.

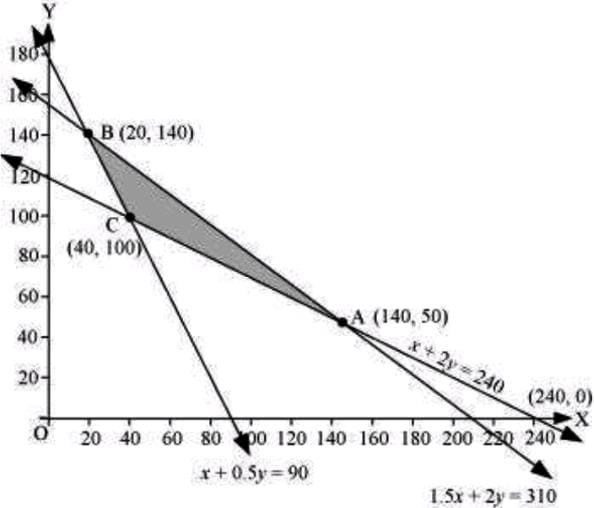
The corner points are A(140, 50), B(20, 140), and C(40, 100). The values of z at these corner points are as follows.

Corner point	z=3x+3.5y
A(140,50)	595	→ Maximum
B(20,140)	550
C(40,100)	470

The maximum value of z is 595 at (140, 50).
Thus, 140 bags of brand P and 50 bags of brand Q should be used to maximize the amount of nitrogen.
The maximum amount of nitrogen added to the garden is 595 kg.

Some linear programming problems have no optimal solution. This can occur when the region determined by the constraints is unbounded.