📌 Example 1. Find the maximum value of z, given:

{	2x+5y≤25 3x+2y≤21 x≥0 y≥0

✍ Solution:
The system of linear inequalities determines a set of
feasible solutions. The graph of this set is the feasible region.

Graph the feasible region determined by the system

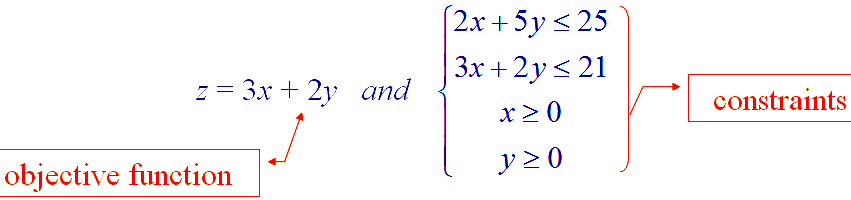
of constraints.

If a linear programming problem has a solution, then the solution is at a vertex of the feasible region.

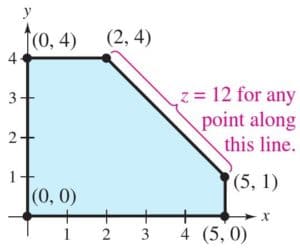
Maximize the value of z= 2x+3y over the feasible region.

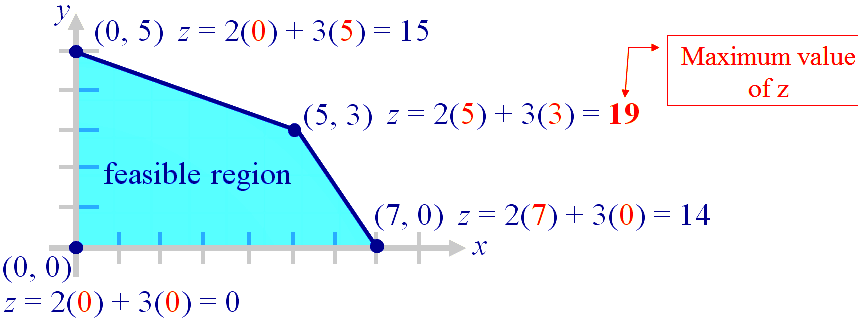
Test the value of z at each of the vertices. The maximum value of z is 19. This occurs at the point (5, 3) or when x=5 and y=3.

📌 Example 2.
Solve the following LPP graphically:
Maximise Z=2x+3y,
subject to x+y≤4, x≥0, y≥0
✍ Solution:
The shaded region (OAB) in the [Fig. Ex2] is the feasible region determined by the system of constraints x≥0, y≥0 and x+y≤4.
The feasible region OAB is bounded, so, maximum value will occur at a corner point of the feasible region.
Corner Points are O(0, 0), A (4, 0) and B (O, 4).
Evaluate Z at each of these comer point.

Corner Point	Value of Z
O(0, 0)	2(0)+3(0)=0
A(4, 0)	2(4)+3(0)=8
B(0, 4)	2(0)+3(4)=12←maximum

[Fig. Ex2]
Hence, the maximum value of Z is 12 at the point (0, 4)

📌 Example 3:
Maximize Z=3x+4y subject to the constraints: x+y≤4, x≥0, y≥0.
✍ Solution:
The feasible region determined by the constraints, x+y≤4, x≥0, y≥0, is as follows.

The corner points of the feasible region are O(0, 0), A(4, 0), and B(0, 4). The values of Z at these points are as follows.

Corner point	Z=3x+4y
O(0, 0)	0
A(4, 0)	12
B(0, 4)	16→Maximum

Therefore, the maximum value of Z is 16 at the point B(0, 4).

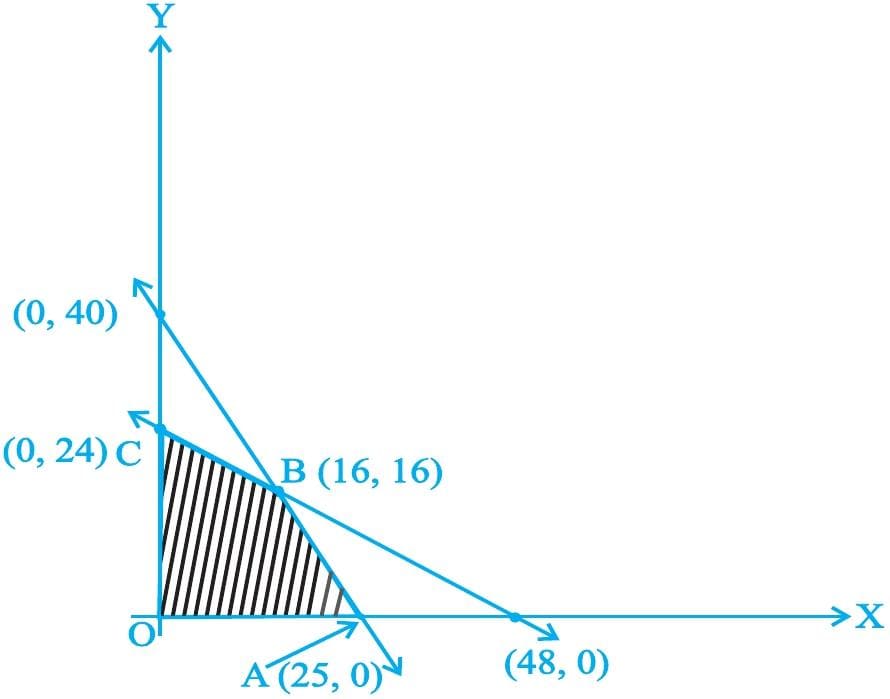
📌 Example 4. Determine the maximum value of Z=4x+3y if the feasible region for an LPP is shown in [Fig. Ex4].
✍ Solution:
The feasible region is bounded. Therefore, maximum of Z must occur at the corner point of the feasible region [Fig. Ex4].

Corner Point	Value of Z
O(0, 0)	4(0)+3(0)=0
A(25, 0)	4(25)+3(0)=100
B(16, 16)	4(16)+3(16)=112←maximum
C(0, 24)	4(0)+3(24)=72

[Fig. Ex4]
Hence, the maximum value of Z is 112.

📌 Example 5.
Solve the following linear programming problem graphically:
Maximise Z=4x+y … (1)
subject to the constraints:

x+y≤50 … (2)
3x+y≤90 … (3)
x≥0,y≥0 … (4)
✍ Solution:
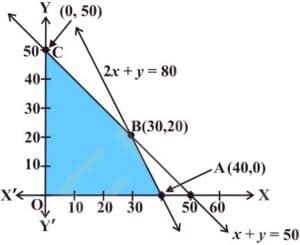
The shaded region in [Fig. Ex5] is the feasible region determined by the system of constraints (2) to (4). We observe that the feasible region OABC is bounded. So, we now use Corner Point Method to determine the maximum value of Z.

The coordinates of the corner points O, A, B and C are (0, O), (30, 0), (20, 30) and (0, 50) respectively. Now we evaluate Z at each corner point.

Corner Point	Corresponding value of Z
O (0, 0) C (30, 0) B (20, 30) A (0, 50)	0 120 ← Maximum 110 50

[Fig. Ex5]
Hence, maximum value of Z is 120 at the point (30, 0).

📌 Example 6:
Maximize Z=5x+3y
subject to 3x+5y≤15, 5x+2y≤10, x≥0, y≥0.
✍ Solution:
The feasible region determined by the system of constraints, 3x+5y≤15, 5x+2y≤10, x≥0, y≥0, is as follows.

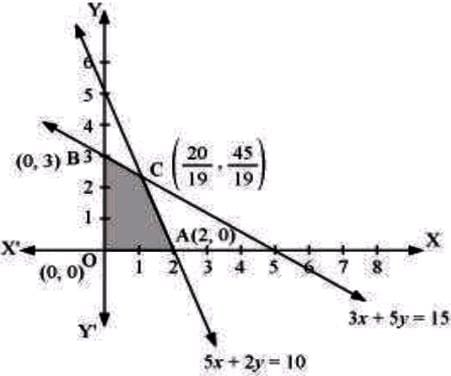
The corner points of the feasible region are O(0, 0), A(2, 0), B(0, 3), and C(20/19, 45/19). The values of Z at these corner points are as follows.

Corner point	Z=5x+3y
O(0, 0)	0
A(2, 0)	10
B(0, 3)	9
C(20/19, 45/19)	(235/19)≅12 [Maximum]

Therefore, the maximum value of Z is 235/19 at the point (20/19, 45/19).

📌 Example 7:
Maximize Z=3x+2y
subject to x+2y≤10, 3x+y≤15, x, y≥0
✍ Solution:
The feasible region determined by the constraints, x+2y≤10, 3x+y≤15, x≥0 and y≥0, is as follows.

The corner points of the feasible region are A(5, 0), B(4, 3), and C(0, 5). The values of Z at these corner points are as follows.

Corner point	Z=3x+2y
A(5, 0)	15
B(4, 3)	18→Maximum
C(0,5)	10

Therefore, the maximum value of Z is 18 at the point (4, 3).

📌 Example 8: Solving a Linear Programming Problem
Find the maximum value of the objective function

z=4x+6y [Objective function]
where x≥0 and y≥0, subject to the constraints

–x+y≤11 x+y≤27 2x+5y≤90

}Constraints

✍ Solution:
The region bounded by the constraints is shown in [Fig. Ex8].

[Fig. Ex8]
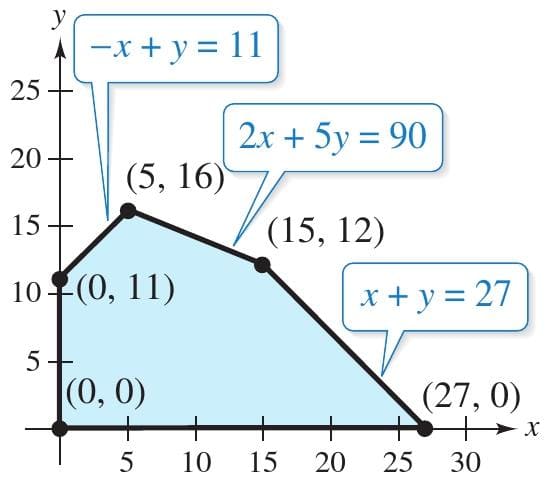
By testing the objective function at each vertex, you obtain

At (0, 0): z=4(0)+6(0)=0 At (0, 11): z=4(0)+6(11)=66 At (5, 16): z=4(5)+6(16)=116 (Maximum value of z) At (15, 12): z=4(15)+6(12)=132 At (27, 0): z=4(27)+6(0)=108.

So, the maximum value of z is 132, and this occurs when x=15 and y=12.
💪 Graphical Method to Solve Linear Programming Problems 💎