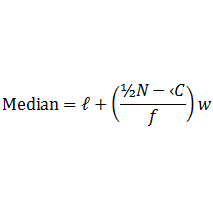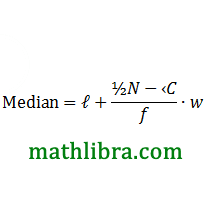How to calculate the approximate mean of grouped data:
● Step 1: Determine the midpoint for each interval.
● Step 2: Multiply the class midpoint by the frequency.
● Step 3: Add up the results from Step 2.
● Step 4: Divide the total from Step 3 by the frequency.
When information has been gathered in groups or classes, we use the midpoint or mid-interval value to represent all scores within that interval.
We are assuming that the scores within each class are evenly distributed throughout that interval. The mean calculated is an approximation of the true value, and we cannot do better than this without knowing each individual data value.
When mid-interval values are used to represent all scores within that interval, what effect will this have on estimating the mean of the grouped data?
Consider the following table which summarises the marks received by Marks I Frequency students for a physics examination out of 50. The exact results for each student have been lost.

What to do:
1. Suppose that all of the students scored the lowest possible result in their class interval, so 2 students scored 0, 31 students scored 10, and so on.
Calculate the mean of these results, and hence complete:
“The mean score of students in the physics examination must be at least ….”
2 Now suppose that all of the students scored the highest possible result in their class interval. Calculate the mean of these results, and hence complete:
“The mean score of students in the physics examination must be at most …. .. .
3 We now have two extreme values between which the actual mean must lie.
Now suppose that all of the students scored the mid-interval value in their class interval. We assume that 2 students scored 4.5, 31 students scored 14.5, and so on.
a) Calculate the mean of these results.
b) How does this result compare with lower and upper limits found in 1 and 2?
c) Copy and complete:
“The mean score of the students in the physics examination was approximately ….”

(A) Discrete Data
Question 1:
Consider the following grouped data and calculate the mean, the modal group and the median group.

solution:
Step 1: Calculating the mean
To calculate the mean we need to add up all the masses and divide by 50. We do not know actual masses, so we approximate by choosing the midpoint of each group. We then multiply those midpoint numbers by the frequency. Then we add these numbers together to find the approximate total of the masses. This is show in the table below.

Step 2: Answer
The mean 2650/50=53.
The modal group is the group 51-53 because it has the highest frequency. The median group is the group 51-53, since the 25th and 26th terms are contained within this group.
Question 2:
Estimate the mean of the following ages of bus drivers data, to the nearest year:

the mean age of the drivers is about 38 years.
(B) Continuous Data
Question 3:
Calculate an estimate of the mean number of fans attending the mighty Preston North End football matches from the following table:

Okay, now do you see a problem here?… Look at the first group… we know there were 5 matches where between 0 and 5 000 people turned up, but we don’t know exactly how many people were at those matches!… One match could have had 1,309… another 4,510.. wejust don’t know!
So… The best we can do is to make an estimate!
And what is our best estimate for that first group?… Well, the MID-POINT… 2,500!
And that is how we calculate an estimate for the mean from grouped data:
1. Work out the mid-point
2. Work out the mid-point×frequency for each group
3. Use this formula:

Question 4:
Fifty shoppers were asked what percentage of their income they spend on groceries.
Six answered that they spend between 10% and 19%, inclusive. The full set of responses is given in the table below.

Calculate the mean percentage of family income allocated to groceries.
solution:
i. Determine midpoints of each interval. Since we do not have the exact values in grouped data, we use these approximations
ii. Add up the frequencies to get the number of items in a data set
iii. Determine the total of all

Question 5:
The table below shows information about the number of hours 120 learners spent on their cell phones in the last week.

a) Identify the modal class for the data.
b) Estimate the mean number of hours that these learners spent on their cell phones in the last week.
Teaching notes:
a) Find the class that has the most number of values.
b) Find the midpoint of the class intervals and multiply by the frequency. Find the total of the products and divide by the number in the data set. Remind learners why they are doing this.
solution:
a) 6<h≤8
b)

Estimated mean x̄=730/120=6.08 hour
Question 6:
The intelligence quotient score (IQ) of a Grade 10 class is summarised in the table below.

a) Write down the modal class of the data.
b) Determine the interval in which the median lies.
c) Estimate the mean IQ score of this class of learners.
solution:
a) Modal class has got the most frequency.
b) Total number of frequencies is 30. Median lies between 15th student and 16th student in the IQ interval 110≤x<120. c) Estimate Mean IQ of students
Question 7:
A learner did a project on climate change. At 14:00 each day, she recorded the temperature (in °C) for a certain town. The information is given in the frequency table below.

a) For how many days did the learner collect the data?
b) Write down the modal class for the data.
c) Estimate the mean of the data.
d) Calculate the percentage of days on which the temperature was at least 28°C.
solution:
a) The number of days =2+4+9+5+7+3=30.
b) Modal is the most frequency.
c) Mean is average of the data. Mean is denoted by x̄.

d) That means that the temperature was in 28≤T<44. Number of days =9+5+7+3=24. The percentage of days =24/30×100%=80%. Question 8: Traffic authorities are concerned that heavy vehicles (trucks) are often overloaded. In order to deal with this problem, a number of weighbridges have been set up along the major routes in South Africa. The gross (total) vehicle mass is measured at these weigh bridges. The histogram below shows the data collected at a weighbridge over a month.

a) Write down the modal class of the data.
b) Estimate the mean gross vehicle mass for the month.
c) Which of the measures of central tendency, the modal class or the estimated mean, will be most appropriate to describe the data set? Explain your choice.
solution:
a) Modal class has got the most frequency. The modal class is 2500≤x<4500. b)

Estimated mean

c) The estimated mean.
It is more at the centre of the data set. The modal class is found at with reason the extreme left-hand side of the data set.