By definition, the sample space contains all possible outcomes of an experiment. So we know that the proba- bility of observing an outcome from the sample space is 1.
We can calculate the probability of the union of two events using:
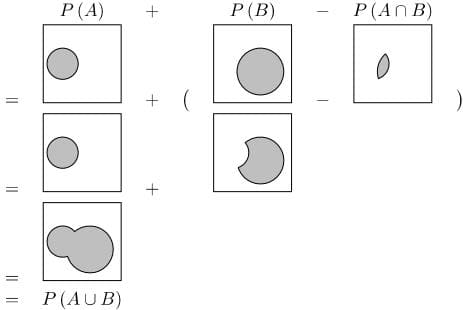
We will prove this identity using the Venn diagrams given above.
For each of the 4 terms in the union and intersection identity, we can draw the Venn diagram and then add and subtract the different diagrams. The area of a region represents its probability.
We will do this for the first column of the Venn diagram figure given previously. You should also try it for the other columns.
The following results apply to probabilities, for the sample space S and two events A and B, within S.
P(A∩B)=P(A)×P(B)
P(A∪B)=P(A)+P(B)-P(A∩B)
Discover Other Set Identities
Q1. P(H)=0.62;P(J)=0.39 and P(H andJ)=0.31. Calculate:
a) P(H’) b) P(H orJ) c) P(H’ orJ’)
d) P(H’ orJ) e) P(H’ andJ’)
solution:
a) P(H’)=1-P(H)=1-0.62=0.38
b) From the addition rule:
=0.62+0.39-0.31=0.7
c) We draw a Venn diagram to get an idea of what the event (H’ orJ’) looks like.
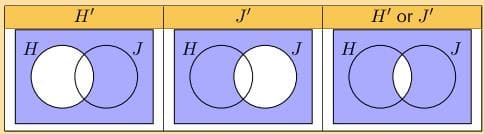
From the third diagram above we can see that
=0.69
d) We draw a Venn diagram to get an idea of what the event (H’ orJ) looks like.
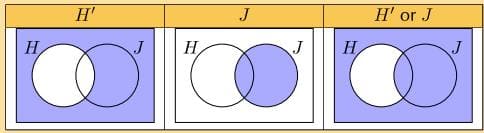
From the third diagram above we can see that
P(H’ orJ)=P(H’)+P(H andJ)
=0.38+0.31=0.69
e) We draw a Venn diagram to get an idea of what the event (H’ andJ’) looks like.
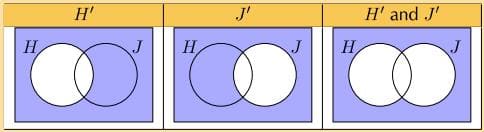
From the third diagram above we can see that
=0.3
Verify that (A∪B)’=A’∩B’.
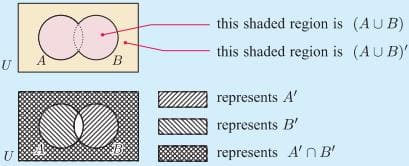
(A∪B)’ and A’∩B’ are represented by the same regions, Verifying that (A∪B)’=A’∩B’.
Q2. The probability that a student will pass the final examination in both English and Hindi is 0.5 and the probability of passing neither is 0.1. If the probability of passing the English examination is 0.75, what is the probability of passing the Hindi examination?
solution:
Let A and B be the events of passing English and Hindi examinations respectively.
Accordingly, P(A and B)= 0.5, P(not A and not B)=0.1, i.e., P(Ā∩B̄)=0.1,P(A)=0.75
Now(A∪B)’=(Ā∩B̄), [De Morgan’s law]
P(A∪B)=1-P(A∪B)’=1-0.1=0.9
We know that P(A or B)=P(A) + P(B)-P(A and B)=0.75+P(B)-0.5
0.9=0.75+P(B)-0.5
P(B)=0.9- 0.75+0.5=0.65
Thus, the probability of passing the Hindi examination is 0.65.
Q3. In a class of 60 students, 30 opted for NCC, 32 opted for NSS and 24 opted for both NCC and NSS. If one of these students is selected at random, find the probability that
(i) The student opted for NCC or NSS.
(ii) The student has opted neither NCC nor NSS.
(iii) The student has opted NSS but not NCC.
solution:
Let A be the event in which the selected student has opted for NCC and B be the event in which the selected student has opted for NSS.
Total number of students = 60
Number of students who have opted for NCC=30
Number of students who have opted for NSS=32
Number of students who have opted for both NCC and NSS =24
(i). We know that

Thus, the probability that the selected student has opted for NCC or NSS is 19/30.
(ii).
=P(Ā and B̄)
=P(Ā∩B̄)
=P(A∪B)’→[(Ā∩B̄)=(A∪B)’]
(by De Morgan’s law)]

Thus, the probability that the selected students has neither opted for NCC nor NSS is 11/30
(iii). The given information can be represented by a Venn diagram as

It is clear that number of students who have opted for NSS but not NCC
=n(B-A)=n(B)-n(A∩B)=32-24=8
Thus, the probability that the selected student has opted for NSS but not for NCC
Q4. A and B are two events such that P(A)=0.54,P(B)=0.69 and P(A∩B)=0.35.
Find (i) P(A∪B) (ii) P(Ᾱ∩B̄) (iii) P(A∩B̄) (iv) P(Ᾱ∩B)
solution:
It is given that P(A)=0.54, P(B)=0.69 and P(A∩B)=0.35.
(i). We know that
P(A∪B)=0.54+0.69-0.35=0.88
(ii). Ā∩B̄=(A∪B)’ [by De Morgan’s law]
= 1-0.88=0.12
(iii). P(A∩B̄)=P(A)-P(A∩B)=0.54-0.35=0.19
(iv). We know that

Q5. Two students Anil and Ashima appeared in an examination. The probability that Anil will qualify the examination is 0.05 and that Ashima will qualify the examination is 0.10. The probability that both will qualify the examination is 0.02. Find the probability that
(a). Both Anil and Ashima will not qualify the examination.
(b). Atleast one of them will not qualify the examination and
(c). Only one of them will qualify the examination.
solution: Let E and F denote the events that Anil and Ashima will qualify the examination, respectively. Given that
P(E)=0.05,P(F)=0.10 and P(E∩F)=0.02
Then
(a). The event ‘both Anil and Ashima will not qualify the examination’ may be expressed as Ē∩F̄.
Since, Ē is ‘not E’, i.e., Anil will not qualify the examination and F̄ is ‘not F’, i.e., Ashima will not qualify the examination.
Also (Ē∩F̄)=(E∪F)’ (by De Morgan’s Law)
Now P(E∪F)=P(E)+P(F)-P(E∩F)
or P(E∪F)=0.05+0.10-0.02=0.13
Therefore
(b). P(atleast one of them will not qualify)
=1-0.02=0.98
(c). The event only one of them will qualify the examination is same as the event either (Anil will qualify, and Ashima will not qualify) or (Anil will not qualify and Ashima will qualify) i.e., E∩F̄ or Ē∩F, where E∩F̄ and Ē∩F are mutually exclusive.
Therefore, P(only one of them will qualify)=P(E∩F̄ or Ē∩F)
=P(E)-P(E∩F)+P(F)-P(E∩F)
=0.05-0.02+0.10-0.02=0.11