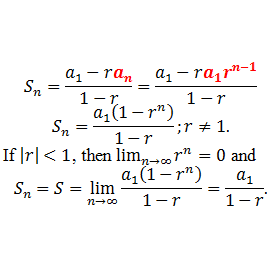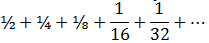Sum of an Infinite Geometric Series
To examine the sum of all the terms of an infinite geometric sequence, we need to consider
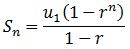
when n gets very large.
|r| is the size of r. |r|>1 means r<-1 or r>1.
If |r|>1, the series is said to be divergent and the sum becomes infinitely large.
For example, when r=2, 1+2+4+8+16+… is infinitely large.
If |r|<1, or in other words -1<r<1, then as n becomes very large, rn approaches 0.
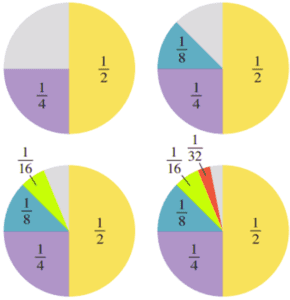
For example, when r=½, 1+½+¼+⅛+… =2.
This means that Sn will get closer and closer to u1/(1-r).
If |r|<1, an infinite geometric series of the form u1+u1⋅r+u1⋅r2+⋯=∑∞k=1 u1⋅rk-1
will converge to the sum
We call this the limiting sum of the series.
This result can be used to find the value of recurring decimals.
Recurring Decimals:
An application of the sum of infinite geometric series is expressing non-terminating, recurring decimals as rational numbers.
Note: The first five letters in the word ‘rational’ spell ‘ratio’. In other words, a rational number is any number that can be written as a ratio (i.e. a fraction).
When we attempt to express a common fraction such as ⅜ or as 4/11 as a decimal fraction, the decimal always either terminates or ultimately repeats.
Thus 0.375=⅜ (Decimal terminate), 4/11=0.363636… (Decimal repeats)
We can express the recurring decimal fraction 0.36 (or 0.3 ̇6 ̇) as a common fraction.
The bar (0.36) means that the numbers appearing under it are repeated endlessly. i.e. 0.36 means 0.363636… .
Thus a non-terminating decimal fraction in which some digits are repeated again and again in the same order in its decimal parts is called a recurring decimal fraction.
Recurring decimals can be expressed neatly by placing a stripe over the first and last figures which repeat.
This is called the overline notation. For example:

💎 Worked Example 1.
Express the recurring decimal 0.13131313… as a proper fraction.
🌪 STEPS:
(1) Express the given number as a geometric series.
(2) State the values of a and r. a=0.13 and r=0.0013/0.13=0.01
(3) find the sum to infinity, S∞

Write the formula for the sum to infinity.
(4) Substitute values of a and r into the formula and simplify.

(5) Multiply both numerator and denominator by 100 to get rid of the decimal point.
📌 Example 1. By writing the recurring decimal 0.12=0.121212… as

express 0.12 as a rational number in simplest form.
✍ Solution:
We can write the decimal 0.12 as

which is a geometric series with a=12/102 and r=1/102. The limiting sum is

📌 Ex2. find the fraction equivalent to the recurring decimals 0.123.
✍ Solution:
Let S=0.123
=0.123+0.000123+0.000000123+⋯
Here a=0.123, r=0.000123÷0.123=0.001

📌 Ex3. Express the recurring decimal 0.73 in the form a/b, where a, b∈N.
✍ Solution:
=0.7+0.03+0.003+0.0003
The series in the brackets is an infinite geometric series, with a=0.03 and r=0.003÷0.03=0.1.

💪 Let’s read post •Writing a Repeating Decimal as a Fraction with three methods👈.