Making solutions with venn diagram is easier than doing without it. We may think harder, If we try to answer advanced-probability questions without it.

Q1. Two events, A and B, are complementary and make up the entire sample space.
Also, P(Ᾱ)=0.35.
a) Complete the statement: P(A)+P(B)=⋯
b) Write down the value of P(A and B).
c) Write down the value of P(B).
answer:
a) P(A)+P(B)=1
b) (A and B)=0
c) P(B)=P(Ᾱ)=0.35

Q2. A group of 45 children were asked if they eat Frosties, Strawberry Pops or both. 31 children said they eat both and 6 said they only eat Frosties. What is the probability that a child chosen at random will eat only Strawberry Pops?
answer:

45(all)-6(only Frosties)-31(both)=8(only Strawberry Pops)
∴8/45=0.18

Q3. In a group of 42 learners, all but 3 had a packet of chips or a cooldrink or both. If 23 had a packet of chips and 7 of these also had a cooldrink, what is the probability that one learner chosen at random has:
a) both chips and cooldrink
answer:

7/42=⅙
b) only cooldrink
answer:
Since 42-3=39 learners had at least one, and 23 learners had a packet of chips, then 39-23=16 learners only had a cooldrink.

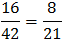
Q4 If you throw two dice at the same time, the probability that a six will be shown on one of the dice is 10/36 and the probability that a six will be shown on both the dice is 1/36. What is the probability that a six will show on neither of the dice when you throw two dice at the same time?
answer:
P(not getting a six)

Q5. If D and F are mutually exclusive events, with P(not D)=0.3 and P(D or F)=0.94, find P(F).
answer:
Since D and F are mutually exclusive, the sum rule for mutually exclusive events applies:
P(D or F)=P(D)+P(F)
We are given P(not D)=0.3, therefore P(D)=1-0.3=0.7. From the sum rule we have
P(F)=P(D or F)-P(D)
=0.94-0.7=0.24

Q6. In a class of 37 children, 15 children walk to school, 20 children have pets at home and 12 children who have a pet at home also walk to school. How many children walk to school and do not have a pet at home?
answer:
Let E be the event that a child walks to school; and let F be the event that a child has a pet at home. Then, from the information in the problem statement

n(E)=15;n(F)=20;n(E and F)=12
We are asked to compute n(E and (not F)).
n(E and (not F))=n(E)-n(E and F)
=15-12=3

Q7. A study was undertaken to see how many people in Port Elizabeth owned either a Volkswagen or a Toyota. 3% owned both, 25% owned a Toyota and 60% owned a Volkswagen. What percentage of people owned neither car?
answer:
Let T be the event that a person owns a Toyota; and V be the event that a person owns a Volkswagen. According to the information in the problem:

P(T and V)=0.03;P(T)=0.25;P(V)=0.6
We are asked to compute P(not (T or V)).
P(not (T or V))
=1-P(T or V) (complementary rule)
=1-(P(T)+P(V)-P(T and V)) (sum rule)
=1-(0.25+0.6-0.03)=0.18

Q8. A group of children were surveyed to see how many had red hair and brown eyes. 44 children had red hair but not brown eyes, 14 children had brown eyes and red hair, 5 children had brown eyes but not red hair and 40 children did not have brown eyes or red hair.
a) How many children were in the school?
answer:
The following possibilities exist for the hair and eye colour surveyed. Each of these is mutually exclusive:
● A child has brown eyes and red hair.
● A child has brown eyes but not red hair.
● A child has red hair but not brown eyes.
● A child does not have red hair or brown eyes.
Since we are given the total number of children in each of these four groups we can add these together to get the total number of children: 44+14+5+40=103.
b) What is the probability that a child chosen at random has:
i. brown eyes ii. red hair
answer:
i. 19/103 ii. 58/103
c) A child with brown eyes is chosen randomly. What is the probability that this child will have red hair?
answer:

💪 How can we Calculate Probabilities without a Two-Set Venn Diagram? 🎓