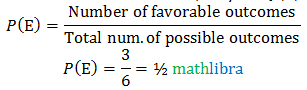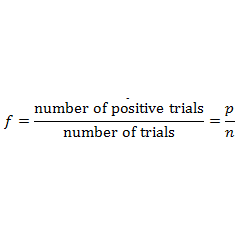Independent Events
Toss A Coin
Q1. A coin is tossed five times. Find the probability of getting five heads.
answer:.
The probability of getting five heads is ½∙½∙½∙½∙½=1/32.

Q2. Determine the probability of getting 2 heads in two successive tosses of a balanced coin.
Solution:
When two coins are tossed then the possible outcomes are

S={HH,HT,TH,TT}
n(S)=4
Let H be the event shows 2 heads getting. Hence
P(H)=n(H)/n(S) =¼

Roll A Die
Q3. A die is rolled twice: Event E₁ is the appearance of even number of dots and event E₁ is the appearance of more than 4 dots. Prove that

P(E₁∩E₁ )=P(E₁ )∙P(E₁ )
Solution:
A dice is rolled twice, so that possible outcomes =36.
E₁= appearance of even number of dots.

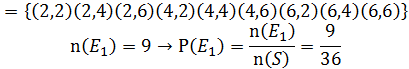
E₁= appearance of more than 4 dots.

Q4. One die is rolled three times. What is the probability that the same number will appear every time?
a. ⅙ b. 1/36
c. 1/216 d. 7/216
correct: b, solution:
Chance of getting a number in a single throw is ⅙ and that in three throws =1/216
Probability of getting any same number three times (that number can be any of the 6 number)
=6×1/216=1/36

Q5. A fair die is thrown twice. Find the probability that a prime number of dots appear in the first throw and number of dots in the second throw is less than 5.
Solution:
When a fair die is rolled then the possible outcomes are

S={1,2,3,4,5,6}→n(S)=6
Let A be the event that a prime number of dots appear
in first throw then the possible favourable outcomes are
A={2,3,5}→n(A)=3
P(A)=3/6=½
Let B be the event that the number of dots in second throw is less than 5, then possible favourable outcomes are B={1,2,3,4}→n(B)=4
P(A)=4/6=⅔
So, the required probability
P(A∩B)=P(A)∙P(B)=½×⅔=⅓

Q6. What is the probability of throwing four 6s in a row with four rolls of a regular die?
Solution:
Each roll of the die is independent of the previous one.

P(four 6s in a row)=⅙×⅙×⅙×⅙=1/1296

Throw Two Dice
Q7. Two dice are thrown twice. What is probability that sum of the dots shown in first throw is 7 and that of the second throw is 11?
Solution:

n(S)=36
Let A be the event that ttle sum of the numbers of dot shown is of then the favourable outcomes are

Let B be the event that the sum of dots shown is 11, then the favourable outcomes are

Hence the required probability:

Q8. Find the probability that the sum of dots appearing in two successive throws of two successive throws of two dice is every time 7.
Solution:
The possible outcomes are n(S)=36
Let A be the event that the sum of numbers of dot shown is 7 then.

Let B be the event that the sum of numbers of dots is 7 the
n(B)=6
P(B)=6/36=⅙
Required probability =P(A∩B)=⅙×⅙=1/36.
Let’s read the post Probability – Independent Events.
Probability with replacement of Dependent Events
Q9. An urn contains three red balls, four green balls, and two blue balls. A ball is selected at random and its color is noted.Then it is replaced and another ball is selected and its color is noted. Find the probability of each of these:
a) Selecting two green balls
b) Selecting a blue ball then a red ball
c) Selecting a green ball then a red ball
Solution:
Since the first ball is being replaced before the second ball is selected, the events are independent.
a) There are four green balls and a total of nine balls; therefore, the probability of selecting two green balls with replacement is
P(green and green)=P(green)×P(green)
=(4/9)×(4/9)=16/81
b) There are two blue balls and three red balls, so the probability of selecting a blue ball and then a red ball with replacement is
P(blue and red)=P(blue)×P(red)
=(2/9)×(3/9)=2/27
c) There are four green balls and three red balls, so the probability of selecting a green ball and then a red ball with replacement is
P(green and red)=P(green)×P(red)
=(4/9)×(3/9)=4/27

Q10. A bag contains 8 red, 5 white and 7 black balls, 3 balls are drawn from the bag. What is the probability that the first ball is red, second ball is white and third ball is black, when every time the ball is replaced?
Solution:
Number of red balls =8
Number of white balls =5
Number of black balls =7
Total balls =20,

n(S)=²⁰C₁ =20
Let A be the event that the ball drawn is red, n(A)=8
Let B be the event that the bell drawn is white, n(B)=5
Let C be the event that the ball drawn is black, n(C)=7
Now

Now the probability that the first ball is the red the second ball is white and the third ball is black when every time the ball is replaced is

Q11. A card is drawn from a deck then replaced, and a second card is drawn.Find the probability that two aces are selected
answer:
The probability that two aces are selected is

Q12. Two cards are drawn from a deck of 52 playing cards. If one card is drawn and replaced before drawing the second card, find the probability that both the cards are aces.
Solution:
Let event A denote that the first Card is ace and event B denote that the second is also ace. Required probability is

Q13. Two cards from a deck of 52 playing cards are drawn in such a way that the card is replaced after the first draw. Find the probabilities in the following cases:
(i). First card is king and the second is queen.
Solution:
Let event A denote that first card is king and event B denote that second card is queen

(ii). Both the cards . are faced cards i.e king, queen, jack
Solution:
Let event K₁ denote that first card is king and event K₁ denote that the second card is also king. So

Similarly let event Q₁ denote that first card is queen and event Q₁ denote that the second card is also queen. So

Similarly let event J₁ denote that first card is jack and event J₁ denote that the second card is also jack. So

Hence, required probability is
P(Both cards are faced cards)

Let’s read these related posts Probability Without Replacement.
Conditional Probability, Chance of Next Event Happening.